ĆWICZENIE NR 49
GONCERZ RAFAŁ
WSTĘP TEORETYCZNY
Drgania relaksacyjne są to drgania do których wykorzystuje się proces ładowania i rozładowania kondensatora poprzez opornik. Napięcie na okładkach kondensatora zmienia się wykładniczo zgodnie ze wzorami :
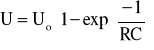
podczas ładowania :
( 1 )
podczas rozładowania :
![]()
( 2 )
Obwód służący do wytwarzania drgań relaksacyjnych zawierać musi element, który samoczynnie reguluje czas trwania ładowania i rozładowania. Jest nim lampa elektroniczna wypełniana gazem, najczęściej neonem (neonówka), zwana stabiliwoltem. Stabiliwolt ma dwie elektrody metalowe pokryte warstwą metalu łatwo emitującego elektrony (np. baru).Jeżeli do elektrod przyłożymy niewielkie napięcie, to prąd nie popłynie. Po przekroczeniu wartości napięcia zapłonu Uz , potrzebnej do wywołania jonizacji lawinowej, przez lampkę popłynie prąd o natężeniu ograniczonym tylko oporem zewnętrznym. Gdy napięcie na elektrodach spadnie poniżej napięcia gaśnięcia Ug , wtedy jonizacja lawinowa wygasa i lampka znowu staje się doskonałym izolatorem. W trakcie żarzenia pomiędzy elektrodami znajdują się ładunki elektryczne, które dają dodatkowy przyczynek do pola przyspieszającego. Z tego względu do podtrzymania jarzenia wystarczy napięcie nieco niższe od napięcia zapłonu. Przepływowi prądu przez lampkę neonową towarzyszy wyładowanie w gazach rozrzedzonych, czyli świecenie.
U
Uz
Ug
T
Wykres zmian napięcia w funkcji czasu podczas ładowania
(linia ukośna) i rozładowywania (linia pionowa) kondensatora.
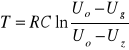
Ze względu na to, że w chwili jarzenia opór jest mały, czas rozładowywania jest bardzo krótki i możemy go zaniedbać (stąd pionowe linie na powyższym wykresie rozładowywania kondensatora).Przyjmujemy więc, że okres drgań jest równy T .
(3)
Bezwymiarowy współczynnik K jest równy :
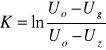
(4)
Ze wzorów (3) i (4) wynika następujący wzór :
![]()
(5)
R
+
+ S stoper
C
~220 V U V
- neonówka
-
Prosty układ do wytwarzania drgań relaksacyjnych
WYNIKI POMIARÓW
|
200 kΩ |
400 kΩ |
600 kΩ |
800 kΩ |
1000 kΩ |
U |
1 μF |
3,1 |
4,9 |
8,3 |
11,5 |
14,4 |
78 V |
2 μF |
5,9 |
11,0 |
16,2 |
22,6 |
28,4 |
U z (śr) |
3 μF |
8,7 |
17,1 |
24,1 |
33,7 |
42,4 |
77 V |
4 μF |
11,5 |
23,2 |
32,0 |
44,8 |
56,4 |
U g (śr) |
5 μF |
14,3 |
29,3 |
39,3 |
55,9 |
70,4 |
72 V |
|
|
|
|
|
|
|
OPRACOWANIE WYNIKÓW
Z otrzymanych wyników obliczam okresy drgań. Oto otrzymane wyniki:
|
200 kΩ |
400 kΩ |
600 kΩ |
800 kΩ |
1000 kΩ |
1 μF |
0,31 s |
0,49 s |
0,83 s |
1,15 s |
1,44 s |
2 μF |
0,59 s |
1,10 s |
1,62 s |
2,26 s |
2,84 s |
3 μF |
0,87 s |
1,71 s |
2,41 s |
3,37 s |
4,24 s |
4 μF |
1,15 s |
2,32 s |
3,20 s |
4,48 s |
5,64 s |
5 μF |
1,43 s |
2,93 s |
3,99 s |
5,59 s |
7,04 s |
Następnie ze wzoru
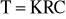
obliczam bezwymiarowy współczynnik K . Oto otrzymane wyniki:
|
200 kΩ |
400 kΩ |
600 kΩ |
800 kΩ |
1000 kΩ |
1 μF |
1,550 |
1,225 |
1,383 |
1,438 |
1,440 |
2 μF |
1,475 |
1,375 |
1,350 |
1,413 |
1,420 |
3 μF |
1,450 |
1,425 |
1,339 |
1,404 |
1,413 |
4 μF |
1,438 |
1,450 |
1,333 |
1,400 |
1,410 |
5 μF |
1,430 |
1,465 |
1,330 |
1,398 |
1,408 |
Obliczam wartości średnie współczynników K ( dla stałej pojemności i zmiennych oporów ) :
dla 1 μF → K = 1,407
dla 2 μF → K = 1,407
dla 3 μF → K = 1,406
dla 4 μF → K = 1,406
dla 5 μF → K = 1,406
Wartość średnia współczynnika K 1,406 0,042
Sporządzam wykres zależności drgań relaksacyjnych od pojemności kondensatora włączonego do obwodu wytwarzającego te drgania (patrz załączony wykres).
Na podstawie zmierzonych napięć zapłonu i gaśnięcia neonówki (wartości średnie) oraz napięcia zasilającego układ wytwarzający drgania relaksacyjne obliczam współczynnik K ze wzoru (4).
Wyliczona wartość współczynnika K wynosi 1,792
WNIOSKI
Sprawdzając zgodność wyliczonych wartości bezwymiarowego współczynnika K (obliczonych ze wzorów (4) i (5) ) zauważamy, że wartości te różnią się. Wartość średnia współczynnika K wyliczona ze wzoru T=KRC wynosi 1,406 0,042, natomiast wartość obliczona niezależnie ze wzoru (4) tj. 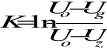
wynosi 1,792. Różnica wynika stąd, że we wzorze (4) nie uwzględnia się zarówno czasu rozładowania kondensatora, który jest bardzo krótki( mały opór podczas jarzenia neonówki), jak i prądu rozładowania, związanego ze stratami kondensatora, co jest źródłem powstawania tej różnicy.
![]()
![]()
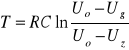
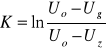
![]()
Wyszukiwarka
Podobne podstrony:
PRAC1FIZ, ĆW 40, I PRACOWNIA FIZYCZNA
PRAC1FIZ, LAB60, I PRACOWNIA FIZYCZNA
PRAC1FIZ, LAB47, I PRACOWNIA FIZYCZNA
PRAC1FIZ, LAB50, SPRAWOZDANIE Z ˙WICZENIA NR 50
PRAC1FIZ, LAB77
PRAC1FIZ, LAB77
PRAC1FIZ, LAB81, I PRACOWNIA FIZYCZNA
PRAC1FIZ, 59WOJ, OPRACOWANIE WYNIKÓW
PRAC1FIZ, KATODOWY, Oscyloskop katodowy
PRAC1FIZ, LAB59, I PRACOWNIA FIZYCZNA
PRAC1FIZ, LAB80, I PRACOWNIA FIZYCZNA
LAB49
LAB49
więcej podobnych podstron