1.HIPOTEZY WYTRZYMAŁOŚCIOWE.
Hipotezy wytrzymałościowe podają kryteria oceny stanu wytężenia materiału w złożonym, trójwymiarowym, stanie naprężenia w celu ilościowego porównania takiego stanu z przypadkiem prostym jakim jest rozciąganie. Naprężeniem zredukowanym (бred)- nazywamy umowne naprężenie otrzymane po zastosowaniu przyjętej hipotezy wytrzymałościowej dla trójwym. stanu naprężenia, które jest równoważne z naprężeniem rozciągającym w jednowym. stanie naprężenia.
1)Hip. największych naprężeń normalnych:.бmax (Ronhine'a):
![]()
2)H. εmax (największego wydłużenia względnego de Saint Venonta)
![]()
3)H.τ max (Coulomba) (największych naprężeń stycznych)
![]()
![]()
4)H-M-H(Huber-Mises-Henchy) w myśl tej hipotezy o wytężeniu materiału decyduje energia odkształcenia postaciowego:
![]()
2.OSIOWO SYMETRYCZNE ZBIORNIKI CIENKOŚCIENNE.
Występujące w wielu konstrukcjach ściany ograniczone mniej lub bardziej zakrywalnymi powierzchniami nazywamy powłokami. Przykładami powłok są: ściany kadłubów silników, pokrycia kadłubów okrętów.
Wzór Laplace'e:
б1/ς1+б2/ς2=ς/б Równanie to ma podstawowe znaczenie w teorii powłok i umożliwia rozwiązanie kilku zagadnień wytrzymałościowych zbiorników cienkościennych.
ZBIORNIK KULISTY-w przypadku powłoki kulistej stosowanej w zbiornikach na gaz, sprężonych do nadciśnienia p, można łatwo określić stan naprężenia biorąc pod uwagę zależności wynikające z warunków symetrii.
б =PD/4 =PR/2 .
ZBIORNIK WALCOWY-o średnicy D, poddany działaniu wew. równomiernego nadciśnienia p. w punktach walcowej części zbiornika z dala od zamykających go dennic, można wyznaczyć naprężenia główne:
б1=PD/2
б 2=PD/4
ZBIORNIK STOŻKOWY-rozpatrujemy powłoki w kształcie powierzchni stożkowej o kącie α pomiędzy tworzącą a osią. Zakładamy, że zbiornik wypełniony jest cieczą o ciężarze właściwym γ i utrzymywany w pionowym położeniu równowagi, równomiernie rozłożonymi siłami działającymi na górne obrzeże zbiornika o kierunkach zgodnych z kierunkami tworzącymi powierzchni stożkowej zbiornika.
3.PODSTAWOWE WŁAŚCIWOŚCI MECHANICZNE MATERIAŁÓW.
Metody badań wytrzymałościowych:
a) próba rozciągania- doświadczenie mające doprowadzić do określenia właściwości mech. materiałów. Podczas próby w maszynie zwanej zrywarką rozciąganiu poddawana jest specjalna próbka o wymiarach określonych normą. Obciążenie zwiększane jest stopniowo. Dośw. kończy się zniszczeniem próbki. Wykres to zależność odkształcenia próbki od jej obciążenia.
b)próba ściskania-przebieg dośw. analogiczny do pr. rozciągania. Czynnikiem utrudniającym realizację próby jest pojawienie się efektu tarcia pomiędzy szczękami a deformowaną próbką. Próba ta jest stosowana do celów technicznych głównie do materiałów kruchych.
c) próba udarności-szybki wzrost działającej na próbkę siły wywołuje znaczne zew. siły bezwładności , które wpływają na przebieg stanu naprężenia. Przebieg dośw. sprowadza się do analizy bilansu energetycznego próby. Podczas dośw. podparta próbka zostaje w środkowym przekroju obciążona udarowo w poruszającym się określoną prędkością ciężkim wahadle młota.
WYKRESY ROZCIĄGANIA
R -granica proporcjonalności -największa wartość naprężenia, przy której zachodzi jeszcze wprost proporcjonalna zależność pomiędzy wydłużeniem i naprężeniem.
R -granica sprężystości -największa wartość naprężenia przy której nie występują jeszcze odkształcenia trwałe.
R -granica plastyczności-wartość naprężenia po osiągnięciu których występują przyrosty odkształcenia przy braku wzrostu naprężenia.
R -wytrzymałość na rozciąganie-wartość natężenia odpowiadająca maksymalnej wartości siły rozciągającej próbkę.
Część wykresu zaznaczona linią przerywaną odpowiada naprężeniom rzeczywistym tj. odniesionym do rzeczywistego chwilowego przekroju próbki rozciąganej.
4.ROZCIĄGANIE I ŚCISKANIE PRĘTÓW PROSTYCH.
NAPRĘŻENIA DOPUSZCZALNE, WSPÓŁCZYNNIK BEZPIECZEŃSTWA.
Wzrost naprężeń i związanych z nimi odkształceń ciała powoduje zmiany w jego stanie fizycznym, które mogą prowadzić do odkształceń trwałych, a nawet zniszczenia spójności materiału. Zmiany te określane są jako wytężenie materiału. Miarą wytężenia w przypadku osiowego działania siły w pręcie jest naprężenie normalne jego przekroju. Maks. wartość jaką może osiągnąć naprężenie б nazywamy naprężeniem dopuszczalnym.
Kr=Rm/nm; Kr=Re/ne;
Kr-wytrz. dopuszczalna na rozciąganie; Kc-wytrz. dopuszcz. na ściskanie; nm- współczynnik bezpieczeństwa. Przyjęcie zbyt dużej wartości współ. bezp. prowadzi do przewymiarowania konstrukcji i związanego z tym zbędnego przyrostu jej masy oraz nadmiernej materiałochłonności.
OBLICZENIA WYTRZ. ZE WZGLĘDU NA NAPRĘŻENIA DOPUSZCZALNE. Podstawą do obliczeń wytrzymałościowych prętów poddanych działaniu siły osiowej jest równanie: б=N/A, gdzie б-naprężenie normalne; N- wartość siły osiowej; A-pole pow. przekroju poprzecznego; oraz warunek: б≤бdop. = Kr
W zależności od tego, która z wielkości rów. jest nieznana rozróżnia się 3 typy obliczeń wytrzymałościowych:
a)oblicz. sprawdzające-polegają na sprawdzeniu, czy spełniony jest war. wytrz.: б=N/A≤Kr;б=N/A≤Kc
b)wyznaczanie obciążenia dopuszcz.-oblicz. polegają na wyznaczeniu dop. wartości obciążenia konstrukcji: Ndop.≤A∗Kr
c)wyznaczenie wymiarów-obliczenia polegają na zaprojektowaniu pola pow. przekroju dla znanego obciążenia i materiału: A≥N/Kr.
5.ANALIZA PRĘTA
UKŁADY STATYCZNIE WYZNACZALNE.
l≤ l dop. -warunek sztywnościowy
Warunek sztywnościowy nie musi być spełniony nawet w przypadku spełnienia warunku wytrzymałościowego, gdyż warunki eksploatacji konstrukcji narzucają ograniczenie jej dopuszczalnych deformacji. Wówczas o wielkości przekroju pręta decyduje warunek sztyw.
a)rozkład sił normalnych:
b)rozkład naprężeń:
c)rozkład przemieszczeń:
UKŁADY STAT. NIEWYZNACZALNE.
Rozpatruję pręt o stałym przekroju poprzecznym dwustronnie utwierdzony, obciążony siłą osiową P
a)metoda przecięć:
b)zasada superpozycji-znajduje zastosowanie w przypadku skomplikowanego układu obciążeń, polega na rozbiciu złożonego układu obciążającego na układy proste, tak dobrane, aby suma tych układów dała rozpatrywany układ wyjściowy.
6.ANALIZA STANU NAPRĘŻENIA
OZNACZENIE SKŁADOWYCH NAPRĘŻEŃ. TENSOR NAPRĘŻEŃ.
W celu określenia stanu naprężenia w ciele konieczna jest znajomość naprężenia w dowolnym przekroju ciała w dowolnym jego punkcie. W celu oznaczenia składowych stanu naprężenia w punkcie wyodrębnia się wokół niego nieskończenie mały prostopadłościan nazywany prostopad. elementarnym. Jeżeli wymiary badanego prostopad. są nieskończenie małe to jednoimienne i równoległe natężenia dla każdej pary ścian równoległych różnią się o nieskończenie małą wartość, a zatem można przyjąć, że są jednakowe.
W prostopadłościanie elementarnym występuje 9 składowych stanu naprężenia: 3 naprężenia normalne i 6 stycznych.
Składowe naprężeń stycznych I do krawędzi przecięcia się 2 przekrojów elementarnych wzajemnie I są zawsze równe. τ =τ ; τ =τ ; τ =τ .
Składowe naprężenia określające stan naprężenia w rozpatrywanym punkcie można przedstawić w postaci macierzy:
Macierz tą nazywamy tensorem naprężeń.
Dla każdego określonego stanu naprężenia można wyznaczyć 3 wzajemnie I osie określające 3 kierunki główne. W odpowiadających im przekrojach wystąpią wyłącznie naprężenia normalne, zwane głównymi. Znajomość kierunków i naprężeń głównych umożliwia określenie stanu naprężenia za pomocą tylko 3 składowych: б ,б ,б .
Naprężenia główne spełniają nierówność: б >б >б
PŁASKI STAN NAPRĘŻENIA.
Jeżeli jedno z naprężeń głównych =0,to stan naprężenia nazywamy płaskim. Płaski stan naprężenia panuje np.: w każdym obciążonym przedmiocie, jego warstwie zew. wolnej od bezpośredniego działania sił zew. Rozpatrujemy prostokątny wycinek ciała o określonej długości, w którym panuje jednorodny, płaski stan naprężenia.
Jeżeli naprężenie styczne na boku o normalnej zew. odpowiadającej jednej z osi układu yz, ma zwrot zgodny ze zwrotem drugiej osi układu, to jest ono naprężeniem dodatnim.
WŁASNOŚCI SKŁADOWYCH PŁASKIEGO STANU NAPRĘŻENIA.
a)naprężenia normalne i styczne w przekrojach równoległych są sobie równe: б =б ; τ =τ
b)naprężenia styczne w 2 wzajemnie I przekrojach są równe co do wartości liczbowej i skierowane do wspólnego naroża lub od wspólnego naroża
c)suma naprężeń normalnych w 2 wzajemnie I przekrojach jest niezmiennikiem układu, oznacza to, że: б +б =б +б =const.
d)jeżeli znane są naprężenia normalne w 2 wzajemnie I przekrojach oraz naprężenie styczne w jednym z nich to stan naprężenia jest jednoznacznie określony.
KOŁO MOHRA DLA PŁASKIEGO STANU NAPRĘŻENIA.
Znamy:ၳy, ၳz, ၴyz
Szukamy: ၳ1, ၳ2, ၡ
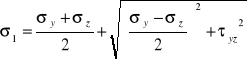
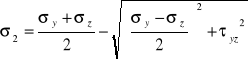
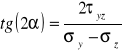
znamy: ၳ1, ၳ2, ၡ
szukamy: ၳy, ၳz, ၴyz
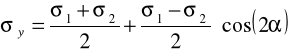
![]()
![]()
ODKSZTAŁCENIA W PŁASKIM STANIE NAPRĘŻENIA.
Odkształcenia na kierunkach głównych wynoszą:
b)
![]()
![]()
![]()
c)
![]()
![]()
![]()
odkształcenia kostki rozciąganej jednocześnie naprężeniami ၳ1 i ၳ2 i są super pozycją w obu powyższych stanach.
![]()
![]()
![]()
Analogicznie dla kostki elementarnej podanej trójkierunkowemu stanowi naprężeń
UOGULNIONE PRAWO HOOKE'A
![]()
![]()
![]()
Analogicznie dla kostki elementarnej poddanej trójkierunkowemu stanowi naprężenia
7.PŁASKI STAN ODKSZTAŁCENIA.
W przypadku, gdy 1 z wymiarów ustroju jest znacznie mniejszy od dwóch pozostałych (np. ustroje płytowe lub tarczowe) odkształcenie na jego kierunku jest pomijalnie małe. Mówimy wtedy o tzw. płaskim stanie odkształcenia.
y, z-odkształcenia liniowe na dwóch wzajemnie prostopadłych kierunkach.
Związki pomiędzy składowymi płaskiego stanu odkształcenia można opisać w sposób analogiczny jak w przypadku płaskiego stanu naprężenia. To koło Mohra dla płaskiego stanu odkształcenia.
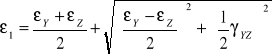
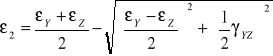
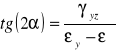
UPROSZCZONA ANALIZA TRÓJWYMIAROWEGO STANU NAPRĘŻENIA.
Rozpatrujemy kostkę sześcienną poddaną działaniu naprężeń głównych б1 ,б2 ,б3 . zakładamy, że б1 Ⴓб2 Ⴓб3 . Trójwymiarowy stan naprężenia można potraktować jako superpozycję 3 stanów płaskich dla 3 wzajemnie I płaszczyzn. W każdym przypadku stan naprężenia można zilustrować kołem Mohra.
Można udowodnić, że przy równoczesnym działaniu wszystkich trzech naprężeń głównych, naprężenia w dowolnym przekroju określone będą odpowiednim punktem N znajdującym się w obszarze zakreskowanym, ograniczonym trzema okręgami Mohra, zbudowanymi dla naprężeń głównych.
8.SKRĘCANIE PRĘTÓW O PRZEKROJU KOŁOWYM.
ZAŁOŻENIA
Jeżeli prosty pręt o przekroju kołowym obciążymy w płaszczyźnie I do jego osi, parą sił o momencie K, wówczas siły wew. w pręcie zredukują się do momentu Ms= K zwanego momentem skręcającym. Gdy na zew. pow. Pręta o przekroju kołowym narysujemy siatkę złożoną z prostych tworzących i kół odpowiadających przekrojom normalnym to pod wpływem działania momentu skręcającego koła te doznają obrotu wokół osi pręta zachowując swoją płaskość, a proste przejdą w linie śrubowe. Mechanizm powstałych odkształceń można zatem wyobrazić sobie jako wzajemne obroty płaskich nie deformujących się przekrojów przy ich wzajemnie nie zmienionych odległościach.
OPIS ODKSZTAŁCEŃ PRĘTA SKRĘCANEGO.
Kąt ![]()
gdzie ![]()
ၲ - zmienna promieniowa
ၮ - współ. Poissona
G- moduł sprężystości postaciowej Kirhchoffa.
.
Kąt skręcania pręta φ jest wielkością charakterystyczną dla określonego przekroju pręta i zależy od współrzędnej x. Można udowodnić, że: ![]()
, ![]()
J0 - biegunowy moment bezwładności
x - długość początkowa pręta
GJ0 - sztywność skrętna pręta
ROZKŁAD NAPRĘŻEŃ W PRĘCIE SKRĘCANYM.
![]()
, ![]()
Wynikiem działania naprężeń ၴၲ działanie na nieskończenie małym elemencie dA przekroju jest elementarny moment skręcający dMs.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
wskaźnik wytrzymałości materiałów na skręcanie
![]()
WSKAŹNIKI WYTRZYMAŁOŚCIOWE PRZEKROJÓW KOŁOWYCH.
![]()
![]()
![]()
![]()
Warunek wytrzymałościowy:
![]()
ks - wytrzymałość dopuszczalna na skręcanie
Warunek sztywności:
![]()
9.ŚCINANIE.
CZYSTE ŚCINANIE
Stanem czystego ścinania nazywamy stan, w którym w rozpatrywanym przekroju ciała występują wyłącznie naprężenia styczne.
Jeżeli rozpatrujemy element myślowo przetniemy prostymi zorientowanymi pod kątem 45 do kierunków głównych to w uzyskanych przekrojach będą występowały wyłącznie naprężenia styczne.
PRAWO HOOKA PRZY CZYSTYM ŚCINANIU
Pod wpływem naprężeń stycznych kąty proste wyodrębnionego elementu ciała ulegną odkrztałceniu o kąt dany.Przekroje elementów pierwotnie płaskie pozostaną płaskie również po odkształceniu.Dla wszystkich materiałów podlęgających prawu Hooka kąt γ jest proporcjonalny do naprężeń stycznych. ![]()
, ![]()
Po odkształceniu podstawa kostki pierwotnej prostokąta staje się rombem.Jejobjętość jest równa iloczynowi pola powierzchni podstawy oraz -wysokości.Bez względu na małą wartość kąta γ pole powierzchni podstawy kostki po odkształceniu jest w przybliżeniu równe jej polu powierzchni przed odkształceniem a zatem oblętość kostki przed odkształceniem jest w przybliżeniu równa objętości kostki po odkrztałceniu.Można zatem stwierdzić że odkształcenie kostki jest odkształceniem postaciowym i -dlatego kąt γ nazywany jest kątem odkształcenia postaciowego a stała materiałowa G modułem sprężystości postaciowej.
![]()
kၴ - wytrzymałość dopuszczalna na ścinanie
![]()
Rt - wytrzymałość doraźna na ścinanie
ht - współczynnik bezpieczeństwa
1)warunek na rozciąganie
![]()
2)warunek na ściskanie
![]()
3)warunek na docisk
![]()
10.ZGINANIE PROSTE
Rozpatrujemy dowolny przekrój popszeczny pręta obciażonego układem sił zew.
Jeżeli siły zew. przekroju redukują sie do wektora momentu gnacego Rg to mówimy że w przekroju tym występuje czyste zginanie. Jeżeli oprócz Mg w przekroju występuje również siła tnąca T to mamy do czynienia z przypadkiem zginania sił poprzecznych.Jeżeli siła tnąca T oraz para sił działaniem których jest moment gnący Mg występuje on w jednej płaszczyżnie zawierające -główne centralne przekrojów poprzecznych pręta to zginanie takie nazywamy zginaniem płaskim lub prostym
Jeżeli siły czynne i reakcje działające na pręt zginany leżą w jednej płaszczyżnie to płaszczyżnę tę nazywamy płaszczyżną zginania.
SIŁĄ TNĄCĄ T - w danym przekroju poprzecznym pręta nazywamy siłę równoważącą rzut na płaszczyżnę tego przekroju ,wypadkowej wszystkich sił zew. działających na część belki odciętej w tym przekroju.
MOMENTEM GNĄCYM Mg - w danym przekroju pręta nazywamy moment równoważący sumę momentów (względem środka ciężkości przekroju) wszystkich sił zew. działających na część belki odciętą w tym przekroju.
Można wykazać żę dla dowolnego przekroju poprzecznego pręta określonego współrzędną x słuszne są związki :
qx =dT/dx
T=dMg/dx
11. PRAWO HOOKA
Wydłużenie jest wprost proporcjonalne do natężenia które jest powodowalne.
(1)
E-jest to modół sprężystości podłużnej (moduł Younga)ModułYounga charakteryzuje odkształcalność materiałów .Wydłużenie poprzeczne jesy wprost proporcjonalne do naprężenia :
(2)
-współczynnik Poissona (wielkość charakterystyczna dla materiału zależy od rodzaju materiału)
Z założenia o płaskości przekroju wynika, że:
(3)
Zatem z równań 1 i 3 mamy:
(4)
Wydłużenie całkowite pręta(z równania:
i równania 4):
Jeżeli N=P=const. , A=const, E=const.
EA-sztywność pręta rozciąganego (ściskanego).
ZASADA DE SAINT VENANTA.
Jeżeli na pewien niewielki obszar ciała sprężystego pozostającego w równowadze działają kolejno rozmaicie rozmieszczone ale statycznie równoważne obciążenia to odległość od tego obszaru przewyższającej wyraźnie jego rozmiary powstają faktycznie jednakowe stany naprężenia i odkształcenia. Jest to zasada sprężystych równoważności statycznie równoważnych układów sił.
12. MOMENTY BEZWŁADNOŚCI WZGLĘDEM OSI RÓWNOLEGŁYCH- TWIERDZENIE STEINERA.
Iy=Iyz+A*a2
Iz=Iyz+A*b2
Iyz=Iyzc+A*a*b
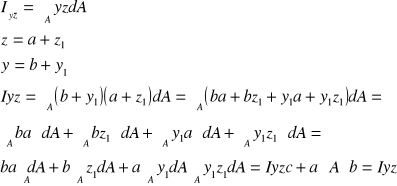
Wyszukiwarka
Podobne podstrony:
wytrzymka ściągi, słupki 1, 1
wytrzymka ściągi, sem2 sciąga, ZGINANIE ZE SKRĘCANIEM
wytrzymka ściągi, wytrz, 1
wytrzymka ściągi, sciąga z wytrzymki w czerni, 1
wytrzymka ściągi, sciąga z wytrzymki w kolorzew, 1
wytrzymałość zmęczeniowa, Transport Polsl Katowice, 4 semesr, moje, PKM, sciagi
sciagi, Automatyka i Robotyka, Semestr 3, Wytrzymałość materiałów, Ściągi
test 3 wytrzymka, Studia, ZiIP, SEMESTR III, sciagi, sciagi
test 2 sciaga wersja deluxe, Automatyka i Robotyka, Semestr 3, Wytrzymałość materiałów, Ściągi
test 2 sciaga wersja mini, Automatyka i Robotyka, Semestr 3, Wytrzymałość materiałów, Ściągi
Wytrzymalosc Materialow - Sciaga(1), NAUKA, budownictwo, BUDOWNICTWO sporo, WILiS, Semestr III, Seme
Wytrzymka - termin I, Automatyka i Robotyka, Semestr 3, Wytrzymałość materiałów, Ściągi
Wzory na ćwiczenia gr. 4, Automatyka i Robotyka, Semestr 3, Wytrzymałość materiałów, Ściągi
mechanika, ściągi, Mechanika wytrzymałości
Wytrzymalosc Materialow - Sciaga(2), NAUKA, budownictwo, BUDOWNICTWO sporo, WILiS, Semestr III, Seme
Wytrzymalosc Materialow - Sciaga(1), ściągi
więcej podobnych podstron