Obciążenia zmienne sinusoidalne.
Takiemu obciążeniu podlega obracajaca się os przy stalej wartości momentu gnacego lub wal maszynowy przy rownie ustalonej wartości momentu gnacego i skręcającego. Obciążenie zmienne sinusoidalne przyjedto za podstawowe do praktycznego wyznaczania zmęczeniowych własności materiałów i elementów modelowych.
W cyklu naprężeń zmiennych sinusoidalnie wyróżniamy:
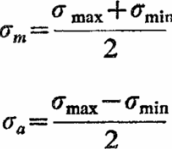
![]()
F= 1/T - częstotliwość zmiany naprężeń.
Rodzaje cykli naprężeń.
Stałe (+/-)
Jednostronny (+/-)
Odzewowo tętniący(+/-)
Wahadłowy
Dwustronny
Wykres Wohlera
jest klasycznym i najstarszym historycznie wykresem zmęczeniowym. Uzyskuje się go w wyniku zniszczenia określonej liczby próbek wzorcowych najczęściej przy zmiennej amplitudzie σ a i ustalonej wartości σ m. każdej wartości σ max= σ m+ σ a odpowiada liczba cykli niszczących N, dopóki amplituda naprężenia σ a nie obniży się do poziomu granicy zmeczenia Zg, przy określonej liczbie cykli Ng.
Granica zmęczenia Zg
największe naprężenie normalne σmax, przy którym próbka lub element nie ulegną zniszczeniu po osiągnięciu umownej granicznej liczby Ng.
Pełny wykres Wohlera
początkiem jest ¼ cyklu, zakłada się równość pomiędzy wytrzymałością zmęczeniową a naprężeniem niszczącym przy działającym obciążeniem statycznym.
I- obszar pękania quasi- statycznego
II- obszar zmęczenia niskocyklowego
III- obszar wytrzymałości wysokocyklowej
Wykres Haigh`a
Wykres Haigha, we współrzędnych σa, σm otrzymuje się na podstawie badan zmęczeniowych dla stałego współczynnika asymetrii cyklu R. każdej parze wartości σa, σm dla danego R odpowiada punkt na wykresie, a polaczenie tych punktow tworzy krzywa.
Punkt A na osi σa określa granice zmeczenia przy obciążeniu wahadłowym (w tym przypadku Zrc). Punkt B na osi σm okresla wytrzymałość przy obciążeniu statycznym (w tym przypadku Rm).
Dla materiałow elastoplastycznych wprowadza się warunek
σ max= σm + σa ≤ Re
określający położenie linii ograniczającej, łączącej wartości Re na obydwóch osiach i odcinającej od punktu D czec wykresu. Pozostaly odcinek krzywej AD zastępuję się odcinkiem prostej. Uzyskano w ten sposób praktyczny wykres Haigha.
Proste wychodzące z początku układu pod katem ω sa miejscem geometrycznym punktów o R= const, przy czym
C - punkt przecięcia prostej pod katem ω z krzywa zmeczeniowa.
Suma rzędnej i odciętej tego punktu jest granicą zmeczenia Z dla danego punktu R, ponieważ
σmax = OE + EC = σm + σa.
Prosta nachylona pok katem 45 stopni do osi σm (jeśli podzialki na osiach sa jednakowe) wyznaczy na krzywej punkt wskazujący współrzędne do obliczenia granicy zmeczenia przy odzerowo tętniącym obciążeniu.
σ a = σm= Zrj/2.
Wykres obejmuję również szeroki zakres σm< 0, jest to symetryczne odbicie prawej części wykresu.
zjawiska zmęczeniowego w metalach
Zjawiska zmęczeniowe w metalach, pomimo ich złożoności, maja pewna okreslona prawidłowość. Wyróżnia się zwykle trzy zasadnicze etapy tego zjawiska:
1 - powstawanie i rozwój lokalnych odkształceń plastycznych oraz z nimi związanego przejściowego umocnienia i osłabienia,
2 - powstawanie mikropęknięć,
3 - rozwoj i laczenie się pęknięć Az do calkowityej dokohezji.
Wizualna oznaką odkształceń plastycznych, obok rzadko występujących bliźniaków, są linie poślizgów i składające się z nich pasma poślizgów. Pojawiają się one podatkowo w ziarnach najdogodniej zorientowanych do działającego układu naprężeń.
Współczynnik α k
Współczynnik α k jest wielkościa związaną wyłącznie z geometrią karbu, nie zależy od wielkości obciążenia, bezwzględnych wymiarów elementu oraz rodzaju materiału w stanie sprężystym. Jest wyznaczany doswiadczalnie za pomocą tensometrów oraz obliczeniowo metodami MES(elementów skończonych) i MEB.(elementów brzegowych)
Współczynnik βk
Współczynnik βk określa wielkość zmniejszenia wytrzymałości zmęczeniowej na skutek działania karbu i jest ustalany na podstawie stosunku wytrzymałości zmęczeniowej próbki gładkiej Zgł do wytrzymałości zmęczeniowej próbki z karbem Zk:
![]()
Podana definicja współczynnika βk nie jest ścisła. W zakresie wytrzymałości quasi-statycznej i niskocyklowej, może się zdarzyć, że βk < 1. Doświadczalne można wyznaczyć βk dla ograniczonej liczby przypadków.
Współczynnik wrażliwości η k
αk i βk łączy współczynnik wrażliwości materiału na działanie karbu ηk, mieszczący się w przedziale 0 ≤ ηk ≤ 1:
Silnej wrażliwości materiału na działanie karbu będzie odpowiadał ηk = 1 i wtedy βk = αk. Cecha ta powinna być właściwa materiałom doskonale sprężystym, umownie doskonale kruchym, których pękanie nie poprzedza odkształcenie plastyczne. Materiałem najlepiej zbliżonym do tych właściwości jest szkło. Brak wrażliwości, czyli ηk = 0, dotyczy materiałów doskonale plastycznych, z pewnym wyjątkiem z grupy materiałów dość powszechnie używanych. Chodzi o żeliwo szare o ηk bliskim zera.
Karby odciążające i przeciążające
Częstokroć spotyka się z kilkoma obok siebie występującymi karbami. Są to karby wielokrotne.
a)karby odciążające- Ich wypadkowe działanie może być słabsze, łagodzące spiętrzenie naprężeń, są nimi zazwyczaj karby szeregowe usytuowane zgodnie z osią obciążenia.
b) karby przeciążające Ich wypadkowe działanie może być silniejsze, powiększające te spiętrzenia w porównaniu z działaniem karbów pojedynczych. Karby położone w poprzek osi obciążenia nazwano karbami równoległymi. Należą one najczęściej do karbów przeciążających.
Kształtowanie elementów maszyn
Aby zmniejszyć wpływ karbu, nadaje się elementom konstrukcyjnym odpowiednie kształty, obniżające spiętrzenia naprężeń.
Niedopuszczalne są nagłe odsadzenia w wałach, osiach, sworzniach bez żadnego odciążenia. Złagodzenie ostrego odsadzenia, jeśli ono jest niezbędne, uzyskuje się przez wykonanie wgłębienia i dodatkowo obrączkowego rowka odciążającego. Przewidując wykonanie wgłębienia, nie wolno zapominać o osłabieniu czynnego przekroju czopa. Kształt rowka odciążającego może być różny od kołowego. Najczęściej łagodzi się część przejściową odsadzenia stosując zarys kołowy, eliptyczny lub dwułukowy o specjalnie dobranych promieniach krzywizny. W tych przypadkach wykonuje się również rowek odciążający.
Złagodzenie części przejściowej powiększa jej długość a skraca ją zarys eliptyczny. Zastosowanie pierścienia dystansowego umożliwia zachowanie zwiększonego promienia przejścia. Wymiary zaokrągleń i podtoczeń wałów dla różnych ciągów średnic łożysk ujmuje norma PN-S5/M-S6413. W ogólności należy unikać stosunku
ၲ/2r ≤ 0,1
poniżej którego spiętrzenie naprężeń szybko rośnie. Ponadto odsadzenia powinny być umocnione przez krążkowanie lub inne zabiegi powierzchniowego ulepszania.
Wpływ stanu warstwy wierzchniej na wytrzymałość przedmiotu
1 - szlifowanych,
2 - starannie toczonych,
3 - zgrubnie toczonych,
βp = βp' = 1 przyjęto dla próbek polerowanych,
Ra - średnie arytmetyczne odchylenie profilu od linii średniej.
Współczynnik βp charakteryzuje zmianę wytrzymałości Z próbki polerowanej w porównaniu z wytrzymałością Zp elementu po różnej obróbce skrawaniem.
βp = Z/ Zp.
Do obliczeń wytrzymałościowych elementów z karbami o współczynniku βk z uwzględnieniem βp posługujemy się zależnością
βk = βk + βk - 1.
W przypadku ostrych karbów współczynnik βp można całkowicie pominąć. Dla żeliwa, po usunięciu naskórka odlewniczego, przyjmuje się βp = 1.
Współczynniki bezpieczeństwa
Współczynnik bezpieczeństwa δ przyjęto nazywać rzeczywistym współczynnikiem bezpieczeństwa, choć nie znane są faktyczne lub nieprzewidzialne warunki pracy układu. Współczynnik δ wskazuje jednak na możliwe odchylenia od przeanalizowanych i przyjętych założeń obliczeniowych. Mówi się o nim, że jest współczynnikiem naszej niewiedzy, od której niezbyt odległa jest obawa o ogólną poprawność obliczeń.
Wartość współczynnika δ przyjmuję się w budowie maszyn najczęściej w przedziale 1,3-2,5 w sposób następujący:
δ = 1,3-1,5 dla wysokiej technologii wykonania
δ = 1,5-1,7 dla zwykłej dokładności obliczeń
δ = 1,7-2,0 dla elementów o większych wymiarach,
δ = 2,0-2,5 przy orientacyjnym określeniu obciążeń i naprężeń,
Naprężenia dopuszczalne
które wyznacza się na podstawie granicy zmęczenia dla danego rodzaju obciążenia i odpowiednio przyjętej wartości współczynnika bezpieczeństwa Xz, obejmującego poznane współczynniki β, ε. δ. Dopuszczalne naprężenie przy wahadłowym zginaniu wynosi:
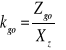
![]()
Xz - ogólny współczynnik bezpieczeństwa, przyjmuje się Xz= 2,5-4.
β i ε - nie są jeszcze znane, ponieważ nie zostały określone wymiary i kształt przedmiotu.
Analogicznie obliczane są dopuszczalne naprężenia dla innych rodzajów obciążenia:
- dla wahadłowego rozciągania- ściskania:
![]()
- dla wahadłowego skręcania:
![]()
- dla cykli odzewowo tętniących:
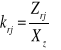
,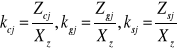
Są to naprężenia dla cykli asymetrycznych. Oznaczenie Zrj, Zcj, Zgj, Zsj dotyczą granic zmęczenia odpowiednio przy: odzewowo tętniącym rozciąganiu, ściskaniu, zginaniu i skręcaniu. Musiał być zatem spełniony elementarny warunek wytrzymałościowy
![]()
Obliczenia zmęczeniowe przy obciążeniach złożonych
W przypadku jednocześnie występujących naprężeń różnego rodzaju, jak no.: od rozciągania do ściskania i zginania lub od zginania i skręcania, naprężenia te składamy tak samo jak naprężenia przy obciążeniu stałym. Stosujemy w tym celu odpowiednią hipotezę wytężenia.
Naprężenia w przekroju karbu składa się tak samo jak naprężenia w przekrojach ciągłych. Ponadto można ze sobą składać tylko te naprężenia, które występują w tym samym miejscu tego samego przekroju elementu i w tym samym czasie. Musi być więc spełniona zasada jedności miejsca i jednoczesności, z którą wiąże się współokresowość naprężeń składowych.
Naprężenia zastępcze dla obciążeń zmiennych niesymetrycznych czy wahadłowych obliczamy tak samo jak dla obciążeń stałych, zgodnie z ogólnymi wyrażeniami :
- przy przewadze naprężeń normalnych
- przy przewadze naprężeń stycznych
Gdzie:
kσ i kγ - naprężenia dopuszczalne dla danego rodzaju obciążenia stałego czy dowolnie zmiennego (kσ - dla rozciągania, ściskania, zginania, kγ - dla skręcania.)
Przy uwzględnieniu działania karbu i wielkości przedmiotu wynika wzór na rzeczywisty współczynnik bezpieczeństwa
Gdzie:
δσ i δγ - składowe rzeczywistego współczynnika bezpieczeństwa obliczone tak, jakby działało tylko zmienne naprężenie normalne lub naprężenie styczne.
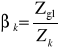
Wyszukiwarka
Podobne podstrony:
Pkm pytania, Transport Polsl Katowice, 4 semesr, moje, PKM
Strona tytułowa - Projekt z wytrzymałości materiałów, Transport Polsl Katowice, 4 semesr, Rok2 TR, p
nasze sprawko, Transport Polsl Katowice, 4 semesr, Rok2 TR, Dioda polprz
pet projekt, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
maksymalny zysk, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
Ściąga egzamin, Transport Polsl Katowice, 4 semesr, PtP egzamin, testy Egzamin
sprawko infa, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
infa sprawko, Transport Polsl Katowice, 4 semesr, Infa program
zad term, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
infa zadania w delphi, Transport Polsl Katowice, 4 semesr, Rok2 TR, Sesja
Sprawozdanie elektronika-bramki, Transport Polsl Katowice, 4 semesr, Rok2 TR, Sesja
Charakterystyka przedsiębiorstwa Projekt 1, Transport Polsl Katowice, 4 semesr, semestr 4
PODSTAWY EKSPLOATACJI TECHNICZNEJ, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
Elektronika II termin ver. 1.1, Transport Polsl Katowice, 4 semesr, Rok2 TR, Sesja
projekt2 PKM, Transport Polsl Katowice, 5 semestr, 5 semestr, PKM projekt
biznesplan OiZ, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
hałas bb, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
6-pomiar mocy za pomocą oscyloskopu, Transport Polsl Katowice, 4 semesr, Rok2 TR, Elektrotechnika
PET mój 2, Transport Polsl Katowice, 4 semesr, 4SEM, IV sem, IV sem
więcej podobnych podstron