1. Wstęp

Statyczna próba rozciągania jest najpowszechniej stosowaną próbą wytrzymałościową przy doborze materiałów na konstrukcje. Jest to próba łatwa do wykonania, dość dokładna i wszechstronna. Próbę tę przeprowadza się zgodnie z normą PN-91/H-04310.

Próby statyczne cechuje mała prędkość wzrostu naprężenia. Wzrost prędkości rozciągania znacznie zwiększa granicę plastyczności metalu, w mniejszym zaś stopniu zwiększa wytrzymałość na rozciąganie.

Podczas statycznej próby rozciągania próbkę poddaje się rozciąganiu za pomocą wolno rosnącej siły F, czemu towarzyszy wzrost długości próbki.

Celem próby statycznego rozciągania jest wyznaczenie:

• umownej granicy sprężystości,

• wyraźnej lub umownej granicy plastyczności,

• wytrzymałości na rozciąganie,

• naprężenia rozrywającego,

• wydłużenia,

• przewężenia,

modułu sprężystości wzdłużnej

2. Metodyka badań

Próbki stosowane do badań są znormalizowane. W naszym przypadku stosowaliśmy próbki o przekroju okrągłym z główkami do chwytania w szczęki. Głównym parametrem próbki, od którego zależą pozostałe wymiary jest wielkość średnicy d₀. Stosowaliśmy próbki pięciokrotne (krótkie), dla których
. Średnica naszej próbki wynosiła d₀ = 8 mm, a więc jej L₀ = 40mm.

Rys. 1 - Próbka zastosowana w statycznej próbie rozciągania

Statyczne próby rozciągania przeprowadza się na tzw. zrywarkach lub rozciągarkach. Próbkę umieszcza się w uchwytach i poddaje wolno zwiększającemu się obciążeniu. Częściej spotyka się zrywarki z napędem hydraulicznym. W naszym ćwiczeniu stosowaliśmy maszynę z napędem mechanicznym.

Silnik prądu stałego poprzez przekładnie i sprzęgła napędza dwie współbieżne śruby pociągowe. Śruby te poruszają dolną belkę w górę lub w dół, powodując ściskanie, albo rozciąganie.

Podczas próby mierzone są dwie wielkości: siłę obciążającą i wydłużenie próbki. Pierwszą wielkość rejestruje wbudowany w maszynę siłomierz, natomiast ekstensometr mierzy wydłużenie. Przyrządy te działają na zasadzie tensometrii oporowej: wraz ze zmianą długości przewodnika zmienia się również jego rezystancja.

Ekstensometr to wygięta w kształcie litery Π blaszka przymocowana do końców długości pomiarowej próbki. Naklejone tensometry służą do odczytu zmian napięcia wraz ze zmianą długości próbki.

Wielkości mierzone przez siłomierz i ekstensometr kierowane są do wzmacniaczy, a następnie do komputera, który tworzy wykres rozciągania F = f(ΔL).

3. Wyniki badań

Statyczna próba rozciągania przeprowadzona została dla próbek okrągłych, proporcjonalnych, pięciokrotnych, dla których średnica początkowa

d₀ = 8 [mm]

Początkowa długość pomiarowa próbki, odpowiadająca sile F = 0

[mm]

Początkowa powierzchnia przekroju poprzecznego próbki:

=
= 50,265 [mm²]

Przeliczenie skali wykresów opisanych zależnością siły obciążającej próbkę F do przyrostu długości odcinka pomiarowego próbki ΔL = L - L₀, na naprężenie umowne
do względnego wydłużenia próbki na odcinku pomiarowym
, gdzie:

[MPa] ;
[%]

gdzie: F - siła obciążająca próbkę [kN]

L - długość odcinka pomiarowego próbki odpowiadająca danej sile F lub naprężeniu
[mm]

Przykłady obliczeń:

F=6 kN
MPa

∆L=4 mm
%

Wyniki przeliczeń:

F=6 kN	=119 MPa	∆L=4 mm	ε=10 %
F=12 kN	=239 MPa	∆L=8 mm	ε=20 %
F=18 kN	=358 MPa	∆L=12 mm	ε=30 %
F=24 kN	=477 MPa	∆L=16 mm	ε=40 %
F=30 kN	=597 MPa	∆L=20 mm	ε=50 %

Dla zamieszczonych w sprawozdaniu wykresów obliczono lub wyznaczono z charakterystyki następujące parametry:

Próbka stopu aluminium (1)

L₀=40 mm L_u=48,4 mm

d₀=8 mm d_u=6,4 mm

S₀=50, 265 mm² S_u=32,17 mm² , gdzie

Własności plastyczne:

1. Maksymalne względne wydłużenie próbki A₅ wyznaczone w oparciu o:

• pomiary
  %

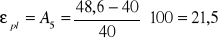
• dane odczytane z wykresu ∆L=8,3 mm

%

2. Maksymalne przewężenie plastyczne (szyjka)

%

Własności wytrzymałościowe:

Zostały wyznaczone na podstawie danych otrzymanych z wykresu

1. Wytrzymałość na rozciąganie (R_m.)

F_m=25,1 kN
MPa

2. Naprężenie rozrywające (R_u)

F_u=22,5 kN
MPa

3. Umowna granica plastyczności (R_0,2)

F_0,2=16,4 kN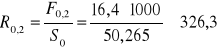
MPa

Próbka stalowa

L₀=40 mm L_u=56,1 mm

d₀=8 mm d_u=4,0 mm

S₀=50, 265 mm² S_u=12,57 mm²

Własności plastyczne:

1. Maksymalne względne wydłużenie próbki A₅ wyznaczone w oparciu o:

• pomiary
  %

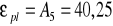
• dane odczytane z wykresu ∆L=14,9 mm

%

2. Maksymalne przewężenie plastyczne (szyjka)

%

Własności wytrzymałościowe:

1. Wytrzymałość na rozciąganie (R_m.)

F_m=21,1 kN
MPa

2. Naprężenie rozrywające (R_u)

F_u=14,9 kN
MPa

3. Wyraźna granica plastyczności (R_e)

Zbadana próbka stalowa ma:

• górną granicę plastyczności (R_eH), odpowiadającą pierwszemu szczytowi obciążenia zarejestrowanemu na wykresie

F_eH=14,6 kN
MPa

• dolną granicę plastyczności (R_eL), odpowiadającą najmniejszej wartości obciążenia na wykresie, z pominięciem pierwszego minimum

F_eL=13,7 kN
MPa

Próbka stopu aluminium (2)

(próbka którą rozciągaliśmy na ćwiczeniach)

L₀=40 mm L_u=47,3 mm

d₀=8 mm d_u=6,6 mm

S₀=50, 265 mm² S_u=34,21 mm²

Mając powyższe dane (bez wykresu) można jedynie wyznaczyć własności plastyczne:

• wydłużenie
  %

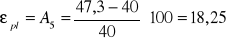
• przewężenie
  %

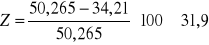
4. Wnioski i spostrzeżenia

Podczas przeprowadzania statycznej próby rozciągania próbki stopu aluminium (AlCu4Mgl) otrzymaliśmy przełom nachylony do osi próbki (kierunku działania siły) pod kątem 45
. Przełom ten nie znajdował się jednak w połowie jej długości pomiarowej, co oznacza, że ewentualny otrzymany wykres nie obrazowałby w pełni własności plastycznych tej próbki. Wartości te byłyby trochę zaniżone. W przypadku stali (St3) otrzymywany przełom jest płaski, prostopadły do osi próbki.

Wykres 1 przedstawiający zachowanie się stopu aluminium (1) podczas statycznego rozciągania nie posiada wyraźnej granicy plastyczności. Wartość naprężenia odpowiadająca umownej granicy plastyczności aluminium, wyznaczona jako siła wywołująca w próbce umowne wydłużenie trwałe ε_pl=0,2% wynosi około R_0,2 = 326,3 MPa. Dokładne określenie tej wartości jest bardzo trudne z powodu małej dokładności początkowej fazy wykresu.

Z kolei na wykresie 2 przedstawiającym zachowanie się stali wyróżnić można górną R_eH = 290,5 MPa i dolną granicę plastyczności R_eL = 272,6 MPa. Są one niższe co do wartości niż w przypadku umownej granicy plastyczności aluminium

W porównaniu z próbką stalową stop aluminium posiada znacznie większą wytrzymałość na rozciąganie rzędu R_m = 499 MPa (wykres jest wyższy), podczas gdy dla stali wielkość ta wynosi 419,8 MPa. Należy jednak zauważyć, że aluminium charakteryzuje się mniejszą niż stal plastycznością (wykres jest węższy - szybciej następuje pęknięcie próbki).

Z wykresów wynika, że wydłużenie obu próbek znacznie się różni. Względne wydłużenie plastyczne stopu aluminium wynosiło około 20,75%, natomiast dla stali było ono prawie dwukrotnie większe 37,25%. Również powstałe na obu próbkach przewężenia mają inne wartości. Dla aluminium Z ≈36%, podczas gdy dla stali wynosi aż Z ≈75%. Potwierdza to fakt, iż wzrost własności wytrzymałościowych odbywa się kosztem obniżenia własności plastycznych materiału (i odwrotnie: wzrost własności plastycznych odbywa się kosztem obniżenia własności wytrzymałościowych).

Na podstawie wykresu zauważamy również, że w zakresie sprężystym aluminium odkształca się bardziej niż stal (początkowy, prostoliniowy odcinek wykresu dla stali jest krótszy, lecz bardziej stromy). Jest to spowodowane różnymi wartościami modułu sprężystości wzdłużnej (modułu Younga), który dla badanej próbki stalowej wynosi E=207000 MPa, zaś dla stopu aluminium E=68000 MPa. Podobnie jak określenie umownej granicy plastyczności dla aluminium, tak i określenie na podstawie otrzymanych wykresów wartości modułu Younga dla obu próbek jest stosunkowo trudne i mało dokładne.

Różnice między wartościami względnego wydłużenia plastycznego otrzymaną na podstawie pomiarów próbki suwmiarką, a wartością odczytywaną z wykresu w niewielkim stopniu wynikają z niedokładności przyrządów pomiarowych oraz samego odczytu. Wynik komputerowy również obarczony jest błędem związanym z niedokładnością zamocowania ekstensometru na końcach długości pomiarowej próbki. Błąd może być spowodowany także samym wyznaczeniem długości pomiarowej próbki i jego naniesieniem.

Zauważono również, że osie wykresów zamieszczonych w sprawozdaniu (są to odbitki wydruków innej grupy) nie są do siebie prostopadłe, co ma wpływ na dokładność odczytania parametrów z charakterystyki F=f(∆L)

1

1

- 1 -

L₀

d₀

---