Zadanie 1. Grupa 6 pracowników, która otrzymała do podziału 4 nagrody w wysokości:
1000 zł, 1500 zł, 3000 zł, 3000 zł
zdecydowała podzielić je między sobą w sposób losowy. Losowanie zorganizowano tak, aby jeden pracownik mógł otrzymać co najwyżej jedną nagrodę.
Niech zmienna losowa X oznacza kwotę jaką w tym losowaniu otrzymał wybrany pracownik.
Wyznaczyć rozkład prawdopodobieństwa zmiennej losowej X,
Wyznaczyć dystrybuantę zmiennej losowej X,
Podać ilustracje graficzną do a i b.
Zadanie 2. Tekla i Zygfryd grają w następującą grę: Tekla rzuca kostką do gry, jeżeli wypadnie liczba mniejsza od 4 - daje Zygfrydowi 2 zł, jeżeli wypadnie 4 lub 5 - nikt nie wygrywa, jeżeli wypadnie 6 - Zygfryd daje Tekli 10 zł. Zmienna losowa X zdefiniowana została jako wartość wygranej Tekli.
Wyznaczyć rozkład prawdopodobieństwa zmiennej losowej X,
Wyznaczyć dystrybuantę zmiennej losowej X,
Oblicz wartość oczekiwaną i wariancję zmiennej losowej X.
Zadanie 3. Zmienna losowa X ma następujący rozkład prawdopodobieństwa:
|
-1 0 1 2 3 |
|
0,2 a 0,1 0,3 0,1 |
Dla jakiej wartości a powyższy rozkład będzie funkcją prawdopodobieństwa?
Przedstawić rozkład na wykresie,
Wyznaczyć dystrybuantę,
Obliczyć momenty zwykłe i centralne do 3 rzędu włącznie, podać interpretacje
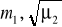
.Obliczyć prawdopodobieństwo przyjęcia przez zmienną losową X wartości:
![]()
, ![]()
, ![]()
Wykorzystaj w tym celu zarówno rozkład prawdopodobieństwa jak i dystrybuantę.
Zadanie 4. Przedstaw momenty centralne, do 4 włącznie, za pomocą momentów zwykłych.
Zadanie 5. Rozkład czasu (w minutach) potrzebnego na wykonanie pewnego zadania przez studentów przedstawia się następująco:
a) 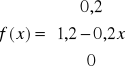
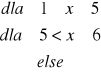
b) 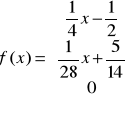
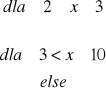
Przedstaw rozkład na wykresie,
Wyznacz dystrybuantę,
Oblicz wartość oczekiwaną i wariancję.
Oblicz prawdopodobieństwo realizacji zmiennej w przedziale 4-6 minut.
Jaki procent studentów wykonuje dane zadanie poniżej 5 minut?
Jaka jest mediana rozkładu?
Co najmniej ilu minut na rozwiązanie zadania potrzebuje 25% najsłabszych studentów?
Zadanie 6. Określ wartość stałej A, tak aby funkcja f była gęstością. Podaj dystrybuantę wyznaczonego rozkładu.
a) 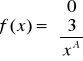
![]()
b) 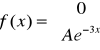
![]()
Zadanie 7. Oblicz wartość oczekiwaną i wariancję zmiennej losowej o gęstości:
a) 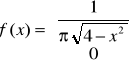
![]()
b) 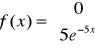
![]()
Zadanie 8. Dobierz tak stałe A i B, by funkcja ![]()
, ![]()
, była dystrybuantą zmiennej losowej. Wyznacz gęstość tej zmiennej losowej. Naszkicuj wykres gęstości i dystrybuanty.
Rachunek prawdopodobieństwa 24-02-09
4
Wyszukiwarka
Podobne podstrony:
Rachunek prawdopodobienstwa cz.1
3 zadania z rachunku prawdopodobieństwa, RACHUNEK PRAWDOPODOBIEŃSTWA CZ
Rachunek prawdopodobieństwa, cz 2
Rachunek prawdopodobieństwa, cz 1
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 6
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 4
Krysicki Rachunek prawdopodobieĹ stwa i statystyka matematyczna cz 1
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 5
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 4
Kombinatoryka Rachunek Prawdopodobieństwa Zadania cz 4
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 2
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 4
Kombinatoryka Rachunek Prawdopodobieństwa Teoria cz 1
więcej podobnych podstron