Rachunek prawdopodobieństwa cz. 3

Rozkłady zmiennej losowej dyskretnej (skokowej:)

zad. 1 Prawdopodobieństwo, że do mieszkańca pewnego rejonu dotrze reklama producenta papieru wynosi 0,20. Jeżeli spośród mieszkańców tego rejonu wybierzemy 10 osób, jakie będzie prawdopodobieństwo, że do co najmniej pięciu z nich reklama dotarła? Jakie będzie prawdopodobieństwo, że reklama dotarła do najwyżej dwóch osób?

zad. 2 Koszykarz został sfaulowany i otrzymał dwa rzuty osobiste. Wiadomo, że trafi on do kosza z prawdopodobieństwem 0,9. Obliczyć prawdopodobieństwo zdarzenia, iż trafi do kosza przy rzutach osobistych co najmniej raz.

zad. 3 Spółka otwiera regionalne biuro handlowe i każdy z dwustu pracowników może zamówić telefon wg własnego uznania. Zakładamy, że na rynku jest dostępnych 1000 modeli telefonów. Jeśli założymy niezależność wyborów i to, że zamówienie któregokolwiek z 1000 modeli jest równie możliwe, jakie jest prawdopodobieństwo, że określony model telefonu zostanie zamówiony przez żadną, jedną, dwie lub trzy osoby z personelu firmy.

zad. 4 Załóżmy, że 35% firm w Wielkiej Brytanii podejmujących ryzykowne przedsięwzięcie jest finansowanych przez spółkę 3i. Oblicz jakie jest prawdopodobieństwo, że wybierając losowo firmy dotąd, aż natrafimy na taką firmę dopiero za trzecim razem?

Rozkłady zmiennej losowej ciągłej: rozkład normalny

zad. 5 Zapisać funkcję gęstości prawdopodobieństwa zmiennej losowej o rozkładzie normalnym, jeśli wiadomo, że wartość oczekiwana i wariancja tego rozkładu wynoszą 2,5.

zad. 6 Naszkicować na wspólnym wykresie współrzędnych gęstości rozkładów:

1. N(2; 2), N(2; 4), N(2; 0,5);

2. N(4; 2), N(4; 4), N(4; 0,5).

Omówić na tej podstawie parametry przesunięcia i skali.

zad. 7 Wartość oczekiwana i odchylenie standardowe zmiennej losowej X o rozkładzie normalnym są odpowiednio równe 15 i 5. Znaleźć prawdopodobieństwo, że X przyjmie wartość:

1. mniejszą niż 12;

2. większą niż 14;

3. należącą do przedziału (12, 14);

4. różną od wartości przeciętnej nie więcej niż o 3.

zad. 8 Dana jest zmienna losowa X o rozkładzie N(5,87; 1,95). Znaleźć prawdopodobieństwo, że X przyjmie wartość:

1. równą 10;

2. nie większą niż 10;

3. należącą do przedziału <2,55; 6,55>;

4. nie mniejszą niż - 5,87.

zad. 9 Zmienna losowa X ma rozkład normalny o funkcji gęstości: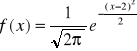
. Obliczyć prawdopodobieństwo, że:

1. P(X<σ);

2. P(‌ X-m‌ <1);

3. P(-2<X<2).

Wyznaczone prawdopodobieństwa przedstawić graficznie, wykorzystać w tym celu wykres funkcji gęstości zmiennej losowej X.

zad. 10 Znaleźć prawdopodobieństwo, że zmienna losowa o rozkładzie normalnym będzie odchylać się od wartości oczekiwanej co najwyżej o kolejne trzy wielokrotności swego odchylenia standardowego. Sformułować na tej podstawie regułę trzech sigm.

zad. 11 Wiadomo, że rozkład IQ (ilorazu inteligencji) dorosłych obywateli USA ma średnią 100, odchylenie standardowe 15 i jest niemal rozkładem normalnym. Załóżmy, że do pracy zgłosił się kandydat o IQ równym 150. Czy jest zasadne stwierdzenie, że jest on wysoce inteligentny? (Przyjmując, współczynnik IQ jako miarę inteligencji.)

zad. 12 Zmienna losowa ma rozkład N(20;5). Jeżeli wiadomo, że zmienna ta przyjmuje wartość:

1. mniejszą od k₁ z prawdopodobieństwem 0,8849;

2. większą od k₂ z prawdopodobieństwem 0,6554;

3. odchylającą się od średniej nie więcej niż o k₃ z prawdopodobieństwem 0,6826;

4. odchylającą się od średniej nie mniej niż o k₄ z prawdopodobieństwem 0,00511;

wyznaczyć nieznane wartości k₁, k₂, k₃ i k₄.

zad. 13 Rozkład miesięcznych dochodów na 1 osobę w rodzinach pracowniczych trzyosobowych jest normalny o parametrach N(580 zł; 100zł). Na podstawie tych informacji obliczyć:

1. prawdopodobieństwo, że w losowo wybranej rodzinie, miesięczny dochód na 1 osobę będzie powyżej 800 zł;

2. ile rodzin, spośród 1000 wybranych losowo, będzie miało miesięczny dochód na 1 osobę poniżej mediany;

3. ile rodzin, spośród 1000 wybranych losowo, będzie miało miesięczny dochód na 1 osobę poniżej 600 zł.

zad. 14 Ustalono, że średni roczny błąd prognozy dochodów pewnej firmy ma rozkład normalny ze średnią 31,3% i odchyleniem standardowym 10%. Załóżmy, że otrzymaliśmy roczną prognozę dochodów firmy.

1. Jakie jest prawdopodobieństwo, że błąd prognozy będzie zawarty między 20% i 25%?

2. Jakie jest prawdopodobieństwo, że błąd prognozy będzie większy niż 50%?

zad. 15 W windach osobowych znajduje się instrukcja o treści „maksymalne obciążenie 7 osób lub 500 kg”. Zakładając, że waga pasażera ma rozkład N(70; 4), policzyć prawdopodobieństwo, że waga siedmiu osób przekroczy dopuszczalne obciążenie 500 kg.

2/2

---