60359

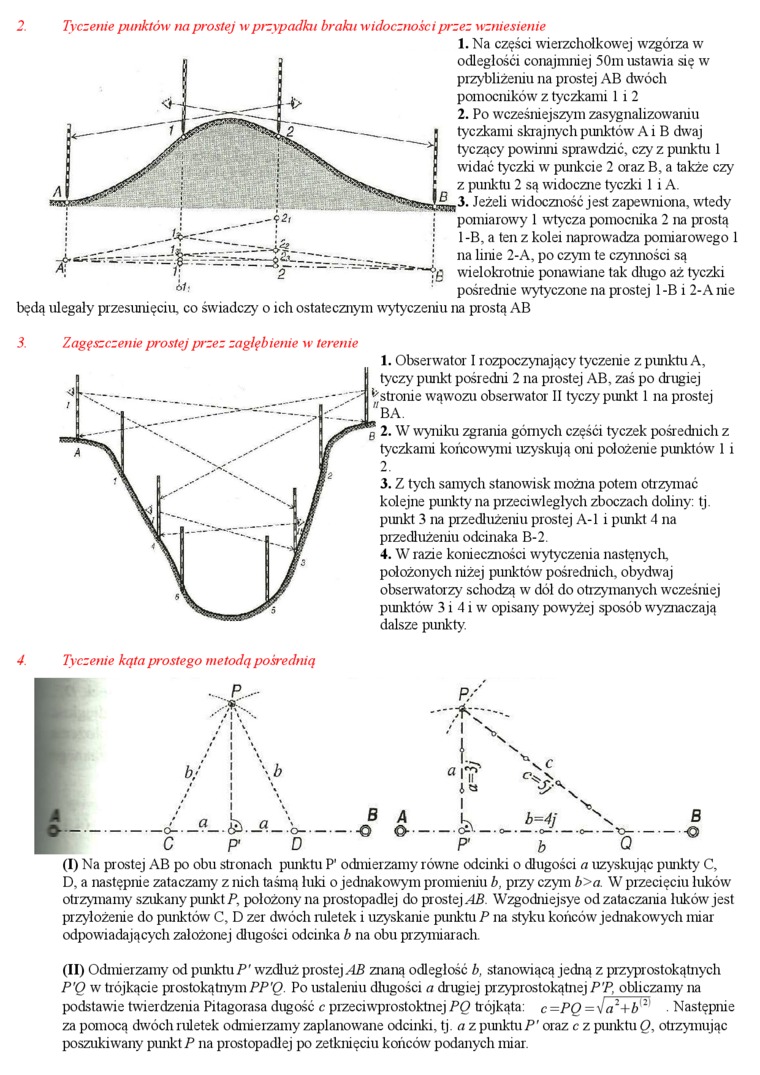
Tyczenie punktów na prostej w przypadku braku widoczności przez wzniesienie

1.    Na części wierzchołkowej wzgórza w odległości conajmiiiej 50ni ustawia się w przybliżeniu na prostej AB dwóch pomocników z tyczkami 1 i 2

2.    Po wcześniejszym zasygnalizowaniu tyczkami skrajnych punktów A i B dwaj tyczący powinni sprawdzić, czy z punktu 1 widać tyczki w punkcie 2 oraz B, a także czy z ptmktu 2 są widoczne tyczki 1 i A.

Jeżeli widoczność jest zapewniona, wtedy pomiarowy 1 wlycza pomocnika 2 na prostą 1 -B, a ten z kolei naprowadza pomiarowego 1 na linie 2-A, po czym te czynności są wielokrotnie ponawiane tak długo aż tyczki pośrednie wytyczone na prostej 1 -B i 2-A nie będą ulegały przesunięciu, co świadczy o ich ostatecznym wytyczeniu na prostą AB

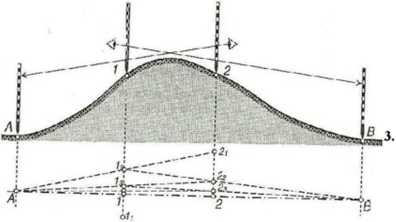
Zagęszczenie prostej przez zagłębienie u terenie

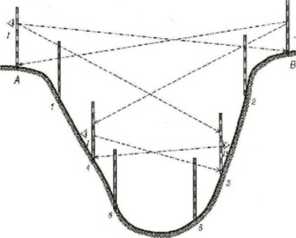
4.    Tyczenie kqta prostego metodą pośrednią

1.    Obserwator I rozpoczynający tyczenie z punktu A, tyczy punkt pośredni 2 na prostej AB, zaś po drugiej

^stronie wąwozu obserwator II tyczy punkt 1 na prostej

'ba.

2.    W wyniku zgrania górnych części tyczek pośrednich z tyczkami końcowymi uzyskują oni położenie punktów 1 i

2.

3.    Z tych samych stanowisk można potem otrzymać kolejne punkty na przeciwległych zboczach doliny: tj. punkt 3 na przedłużeniu prostej A-l i punkt 4 na przedłużeniu odcinaka B-2.

4.    W razie konieczności wytyczenia nastęnych, położonych niżej punktów pośrednich, obydwaj obserwatorzy schodzą w dól do otrzymanych wcześniej punktów 3 i 4 i w opisany powyżej sposób wyznaczają dalsze punkty

A

O-

A

O-

B

■O

(I) Na prostej AB po obu stronach punktu P’ odmierzamy równe odcinki o długości a uzyskując punkty C,

D, a następnie zataczamy z ruch taśmą luki o jednakowym promieniu b, przy czym b>a. W przecięciu luków otrzymamy szukany punkt P, położony na prostopadłej do prostej AB Wzgodrriejsye od zataczania luków jest przyłożenie do punktów C, D zer dwóch ruletek i uzyskanie punktu P na styku końców jednakowych miar odpowiadających założonej długości odcinka b na obu przymiarach.

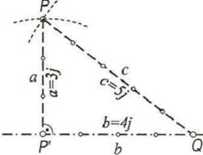
(II) Odmierzamy od punktu/” wzdluz prostej ,4B znaną odległość b, stanowiącą jedną z przyprostokątnych P'Q w trójkącie prostokątnym PP'Q. Po ustaleniu długości a drugiej przyprostokątnej P'P, obliczamy na podstawie twierdzenia Pitagorasa dugość c przeciwprostoktnej PO trójkąta: c=PQ ='ja^:+b ²' Następnie za pomocą dwóch ruletek odmierzany zaplanowane odcinki, tj. a z punktu P’ oraz c z punktu Q, otrzymując poszukiw'any punkt P na prostopadłej po zetknięciu końców podanych miar