60830

Stale dielektryczne: szkło - k, =6 , mika - k₂=7,6 (nie jestem pewien tych wartości, sprawdźcie gdzieś).

C“

Przenikalność elektryczna próżni: e_o=8,85-10    -= .

N'tn

Podstawiając dane:

18,53-10 ^I2F = 18,53pF

6-7,6-8,85-l(T^l2-^-0,009/w² _c=_N-m‘

0,02 /w-6 +0,01 w 7,6

r² r² c

Jednostka: [C]=—-=—■=—-F Nm J V

12. Elektron o szybkości początkowej równej żeni przebył różnicę potencjałów 25kV , a następnie wleciał w przestrzeń między okładki kondensatora płaskiego, w równej odległości od okładek i równolegle do nich. Po wyjściu z kondensatora elektron pada na ekran, który znajduje się w odległości 0,75 m od kondensatora. Znaleźć otrzymane na ekranie odchylenie elektronu od początkowego kierunku mchu. Dhigość okładek kondensatora 25 cm , odległość między nimi 3 cm . Kondensator naładowany byl do różnicy potencjałów 200 V .

U,-25kV , L*=0,75/w , L, = 0,25/;/ , rf=0,03w , £/,= 200F

Najpieiw trzeba policzyć z jaką prędkością elektron wleciał między okładki kondensatora. Mamy pole elektryczne, w którym istnieje różnica potencjałów między dwoma punktami. Pole przenosząc ładunek między tymi punktami wykonuje pracę W równą zmianie energii kinetycznej ładunku, a ponieważ początkowo ładunek spoczywał, więc: E_k-W . Związek między pracą i różnicą potencjałów: W-qU =>E_k-qU .

Znając energię kinetyczną można obliczyć prędkość z jaką elektron wleci między okładki E_k-—mv\ ( v_x oznacza składową prędkości równoległą do okładek, a v_v prostopadłą)

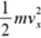
<lU i

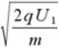
Kiedy elektron wleci między okładki kondensatora, będzie na mego działało jednorodne pole elektryczne. Ponieważ wektor E będzie prostopadły do okładek, więc i działające siły będą prostopadle, a to oznacza, że składowa prędkości v, się nie zmieni. Dzięki temu wiemy, że wzdłuż kierunku równoległego do okładek elektron porusza się z mchem jednostajnym i możemy obliczyć czas, po jakim opuści kondensator.

L. -v,/=>/-—^m , gdzie L_y to długość okładek. v, \2qU_x

W tym czasie pole wewnątrz kondensatora będzie odchylało tor ruchu elektronu. Znając różnicę potencjałów na okładkach i odległość między mmi, możemy obliczyć, jakie jest natężenie pola:

U 2

U ₂-Ed => E-—J-a

Znając natężenie, wiemy, jakie siły działają na elektron: