65660

A. Zaborski. Zginanie ukośne

naprężenia normalne:

M,    A/,    . .

a_x = —^L x₂ + —- . skąd: J\    A

a\ =—⁸³⁹’⁶-—x0.676xl(T²--^S43--x(-102S)xl0~^: = 240xl0⁶ Pa = 240MPa .

17.48x10-*    5.3x10*

a: =—⁸³⁹⁶ . x2.848xl0~^;--— ² -xl.334xl(T² »0,

17.48x10

5Jxl()

a] =—^{839 6} ■„ x(-3.523)xlO~^ł--^{543 2} . x0.6902xl0~² = -240xl0⁶ Pa > -240MPa .

5.3x10

Wizualizacji naprężeń można dokonać na dwa (równoważne) sposoby:

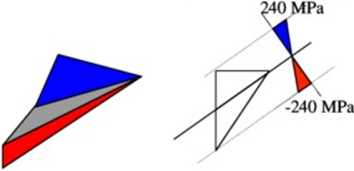
bryła naprężenia

rozkład naprężenia

17.48x10

Przykład

300 MPa:

Zaprojektować pr/.ekrój. przyjmując R

200 kNm

Rozwiązanie:

1.    położenie środka ciężkości: y_c = 1.17 a. /_K = 2.17 a

2.    centralne momenty bezwł.: J> = 30.75 a⁴, J, = 10.75 a⁴. Jy* = -10 a⁴

3.    wartości własne: J| = 34.89 a⁴. J? = 6.61 a⁴, kierunki główne: a = 22.49°

4.    momenty zginające: Mi = Mcosa = 185 kNm, M: = M sina = 76.5 kNm

_c ,, ,    * .    .    .    A/,    A/,    5.30x, +11.57jt, _aJ

5. rozkład naprężeń normalnych: rr, = —+—^Łar, =-*— -^L10

J_t J₂    a

6.    położenie osi obojętnej: X: = -2.19 xi

7.    współrzędne naroży przekroju w układzie głównym ze wzoru transformacyjnego

X| = y cosa + z sina. X2 = -y sina + z cosa Punktem, w którym wystąpią maksymalne naprężenia normalne jest punkt najbardziej

pkt	y	z	xl	x2	odl. od osi oboj.	o | MPa |
A	-1.17 a	-2.17 a	-1.91 a	-1.56 a	2.39 a	-243
B	2.83 a	-2.17 a	1.78 a	-3.09 a	0.34 a	35
C	2.83 a	-1.17 a	2.17 a	-2.16 a	1.07 a	109
D	-0.17 a	3.83 a	1.31 a	3.60 a	2.69 a -> maks.	274
E	-1.17 a	3.83 a	0.38 a	3.99 a	2.01 a	205

8. projektowanie przekroju: O_x( 1.31 a. 3.60 a) £ R => a £ 0.0485 m = 0.05 m