55425

Zadanie 1

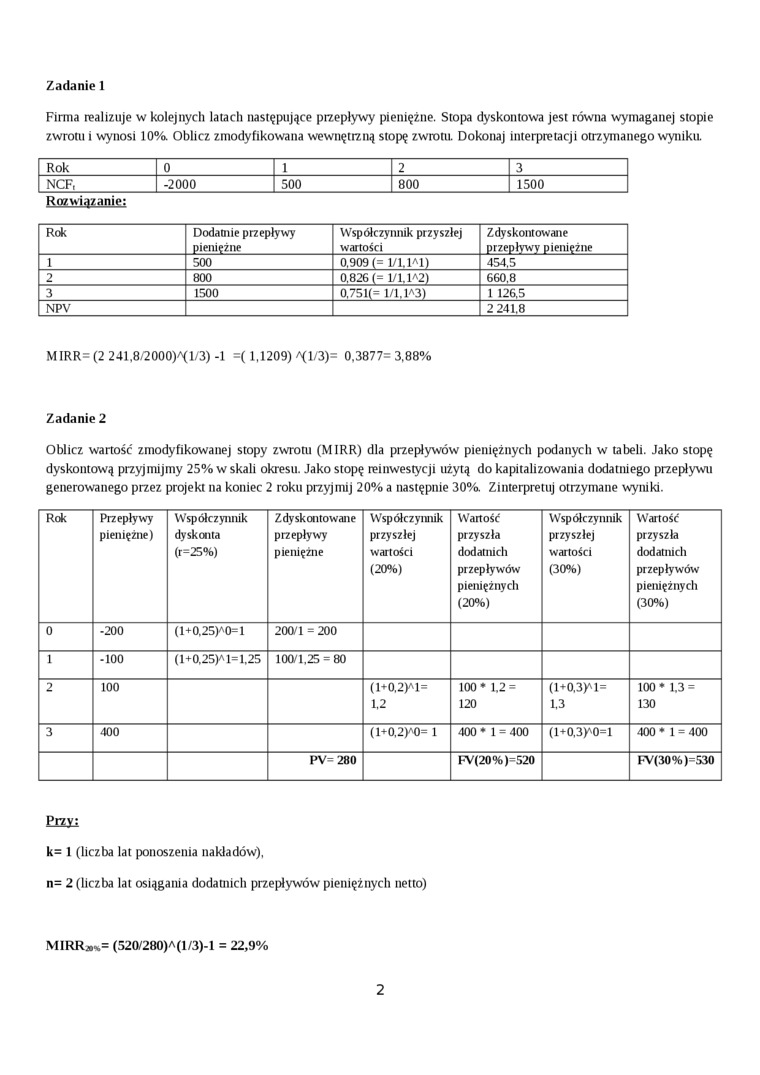
Firma realizuje w kolejnych latach następujące prcepływy pieniężne. Stopa dyskontowa jest równa wymaganej stopie zwrotu i wynosi 10%. Oblicz zmodyfikowana wewnętrzną stopę zwrotu. Dokonaj interpretacji otrzymanego wyniku.

Rok	0	1	2	3
NCF,	-2000	500	800	1500

Rozwiązanie;

Rok	Dodatnie przepływy pieniężne	Współczynnik przyszłej wartości	Zdyskontowane przepływy pieniężne
1	500	0.909 (= 1/UM)	454.5
2	800	0.826 (= 1/1.1^A2)	660.8
3	1500	0,751(= 1/1,1^A3)	1 126,5
NPV			2 241.8

MIRR= (2 241.8/2000)^1/3) -1 =( 1,1209) ^1/3)= 0.3877=3.88%

Zadanie 2

Oblicz wartość zmodyfikowanej stopy zwroni (MIRR) dla przepływów pieniężnych podanych w tabeli. Jako stopę dyskontową przyjmijmy 25% w skali okresu. Jako stopę reinwestycji użytą do kapitalizowania dodatniego przepływu generowanego przez projekt na koniec 2 roku przyjmij 20% a następnie 30% Zinterpretuj otrzymane wyniki.

Rok	Przepływy pieniężne)	Współczynnik dyskonta (r=25%)	Zdyskontowane przepływy pieniężne	Współczynnik przyszłej wartości (20%)	Wartość przyszła dodatnich przepływów pieniężnych (20%)	Współczynnik przyszłej wartości (30%)	Wartość przyszła dodatnich przepływów pieniężnych (30%)
0	-200	(1+0.25^0=1	200'1 = 200
1	-100	(1+0,25^1=1,25	100/1,25 = 80
2	100			(1+0.2)^A1= 1,2	100 ♦ 1.2 = 120	(1+0.3^ 1= 1,3	100* 1.3 = 130
3	400			(1+0,2>^A0= 1	400 ♦ 1 = 400	(1+0,3>^A0=1	400 ♦ 1 = 400
			PV= 280		FV(20%)=520		FV(30%)=530

Przv:

k= 1 (liczba lat ponoszenia nakładów),

n= 2 (liczba lat osiągania dodatnich przepływów pieniężnych netto)

MIRR»*= (520/280) ^A(l/3)-l = 22,9%

2