68753

Nrćw. 101	Data 16-12-94	JACHIMOWIC2 PAWEŁ	Wydział EleWryczny	Semestr HI	Grupa I-I
Prowadząca: mgr hfcgdalena Elantowska			Przygotowanie	Wykonanie	Ocena

Temat: Wyznać tanie przyspieszenia ziemskiego za pomocy wahadła reuersyjnego.

1.    Wahadło fizyczne

Wahadła fizyczne i matematyczne wykonują ruch drgający pod wpływe m dz ńłającej sły c iążkośc i W z akresie niedużych amplitud ruch ten jest mchem harmonicznym, jego okres zależy od Jasności dane go w aha dł a jak również od przyspieszenia ziemskiego.

A

\

\

♦Al \

v-'

T *9

Po wychylę nil z położenia równowagi na cało działa moment sfly ciężkości: męL sin Stosując II zasadą dynamiki do te j sytuac ji otrzymamy:

= mgL sin <p

(i).

gdzie:

I- momentbezwładnościcńła wzglądem punktu zawieszenia A, f • kąt wychylenia odprtożenia równowagi,

L - odległość odpunktu zawieszenia A do środka ciążkości C. 2nak minus wskazuje, że moment siły zawsze stara sią zmniejszyć wychylenie ciała.

2.    Fiichharmonrzny

Ogólne równanie ruchu harmonie zne go:

d*<P •%

—~ ~-of<p    (2), gdzie <o je st prą dkoscią kątową

dO

Pamiątając, że kryterium harmoruczności ruchu opijanego równaniem (l)bądzie spełnione tylko w z akresie małych wychyleń, dla których $m<p = <p. Porównując je z równaniem (2) otrzymujemy wyrażeni określając* okres wahadła fizycznego:

T-2

P),

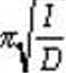
gdzie D=ntyLjest momentem kierującym

3.    Wahadło matematyczne

Wahadło matematyczne różni sią tym od fizyczne go, że cała masa układu jest kupiona w jednym punkcie (który jest oczywiście środkiem ciążkości). Połączenie pom^dzy środkiem ciążkości a punktem zawieszenia interpretuje sią jako nieważką nic o długość i 2. Okres drgań takie go wahadła wyraża sią wzorem:

(4)

4.    Długość zre dukowana wahadła f izyc zne go. Wahadło rewersy jne

Taka długość wahadła matę maty: zne go, dla które go okresy drgań wahadła matematycznego i fizycznego są równe nazywa sią długością zredukowaną wahadła fizyczne go i wynosi ona:

mL

Jeże li znamy długość zredukowani, wahadła fizycznego, wówczas jego okres drgań możemy znaleźć za pomoc ą równania (4); nie jest do tego konieczna znajomość ani momentubezwładnośc i, ani momentu kierujące go. D o wyznacz enia długości zredukowanej wahadła fizycznego wykorzystuje my? tą jego własność, że wahadło zawieszone w punkcie A, anastąprde w punkcie Bposiada ten sam okres jeżeli odległośćpomiądzypunktami zawieszenń jest długością zredukowaną.

Aby wykazać powyższą własność należy znaleźć warunki dh których możliwa jest równość okresów: