85857

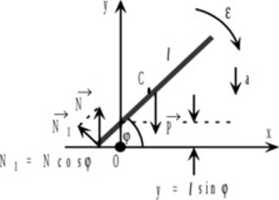
Dynamiczne równanie mchu postępowego belki w kierunku pionowym: am = P-N, P = mg — am = mg - N (1)

Dynamiczne równanie mchu obrotowego belki względem środka masy (C): el = (Ncostp)/

I - moment bezwładności belki względem jej środka, I =-^m(2/)² = ^m/²

c^mi² = N/cosip (2)

£ - przyspieszenie kątowe belki

Jak pokazano na ostatnim rysunku: y = / sintp Różniczkujemy dwukrotnie po czasie ostatnie równanie:

- S=^^sin,{* 1 ^+,cosi^)

_ .    . d²y    dtp    d²(p

Ponieważ: —f =a , — =<o, —=e dt²    dt    dt²

Otrzymujemy: a =/(ecos<p— co²sinq>) i podstawiamy do równania (1)

m/(ecos<p— 6>²sin(p) = mg — N (3)

,    3Ncosq> ,    ,

ml

Wyznaczamy z równania (2) £: e =--— i podstawiamy do równania (3)

ml

( 3Ncos²q> mi

—<o²sinę> j= mg — N

N||^.

W chwili uwolnienia belki <p = <p₀ = 7t/3, natomiast w = 0, stąd otrzymujemy: N =