90405

Wstawiając do pierwszego równania pozostałe otrzymuje się: y*T+i=oyi+(l-a)y*T=ayrK 1* a)[ay_T-1 +(1 -a) {ay_T-2+( 1 -a)(ay_T-3+...)} ]=

=ayr^fa( i -a)yT-1+a( 1 -a)²yr.2+. ■ ⁺a( 1 -a)‘yT-,+...

Jak z powyższego wynika, obserwacji, której wiek wynosi „t”, przyporządkowana jest waga opisana równaniem wykładniczym: w,=a(l-a)¹ gdzie: 0<a<=l

Dla ostatnie, najświeższej zaobserwowanej war tości zmiennej prognozowanej t=0.

Wagi tworzą szereg geometryczny zbieżny postaci: a+a(l-a)+a(l-a)²+a(l-a)³+.. +a(I-a)ⁿ+... których suma jest równa a/[ 1 -(1 -a)]=l

W metodzie wyrównywania wykładniczego prostego, dużą rolę odgrywa stała wygładzania a. Zależność przyjętej wartości współczynnika a od wieku obser wacji zamieszczono na rysunku (rys. własny:)):

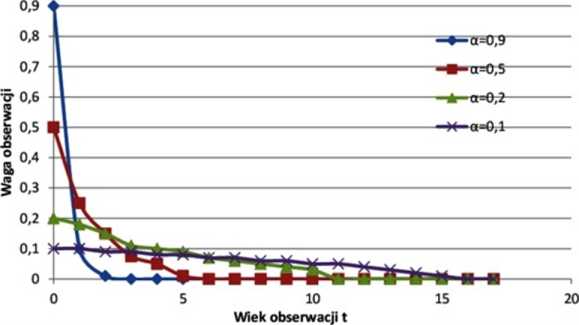
Jeśli a jest bliskie 1, wówczas udział ostatniej obserwacji w prognozie jest większy niż pozostałych obserwacji, a wahania w szeregu czasowym prawie nie ulegają wygładzeniu. Jeśli a jest bliskie 0, wówczas wagi poszczególnych obserwacji nie różnią się wyraźnie między sobą, natomiast szereg ulega wygładzeniu.

Przed rozpoczęciem procedury prostego wygładzania wykładniczego należy przyjąć tzw wartość początkową, czyli yY Zwykle przyjmuje się y*i=yi lub y*i=śr. y Im dłuższy szereg czasowy, tym wartość początkowa wywiera mniejszy wpływ na poziom prognozy. Wartość stałej wygładzania jest przyjmowana w zależności od tego, jak silny ma być efekt wygładzania szeregu czasowego.