252
(b) Przy s = const z równania (8.2.16) otrzymuje się

Gdy cM ~ const w badanym zakresie temperatur, to
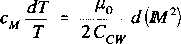
czyli po całkowaniu

ln
T
J3
2 C c
^CWCM
47t 10“7-24,942

Dla małych argumentów funkcji eksponencjalnej można przyjąć, że e x ~ 1 - co daje
T
« 1 - 2,513-lO'6
AT2,3 = T3 T2 = -2,513-lO'6* 700 = -0,00176 K
Przykład 8.2.5
Wyprowadzić równanie adiabaty dla paramagnetyku podlegającego prawu Curie.
Rozwiązanie
Ponieważ w izentropie równanie (8.2.16) redukuje się do postaci
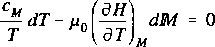
to dla paramagnetyku opisanego równaniem Curie, w którym

dH] = M 3T)m " Cc’
zależność ta przekształca się do postaci
A d(M2) = o
c T3 2 Cc
252
Wyszukiwarka
Podobne podstrony:
skanuj0079 2 154 S. RAmiowajp jonowe w rołtteńczonycfa rołtworach wodnych a uwzględniając równanie (
Po scałkowaniu powyższego wyrażenia przy założonej stałości EA otrzymuje się (7.3.4) gdzie / jest
WM010 Przy jednakowych znakach Ma i z otrzymuje się dodatnią wartość naprężenia normalnego <r, pr
66 (136) 66 2. Przekrój poziomy - otrzymuje się, gdy płaszczyzna przekroju
Wstawiając do pierwszego równania pozostałe otrzymuje się: y*T+i=oyi+(l-a)y*T=ayrK 1* a)[ayT-1 +(1 -
WM010 Przy jednakowych znakach Ma i z otrzymuje się dodatnią wartość naprężenia normalnego a, przy r
img042 96 Z równania (3.101) otrzymują się wartość średnią prądu wyprostowanego prostownika ?-pulsow
- 362 - , ł601 Z tablicy 16 [4] otrzymuje się wartość qv = 2592 kJ/m i, Wstawiając
Wstawiając do pierwszego równania pozostałe otrzymuje się: y*T+i=oyi+(l-a)y*T=ayrK 1* a)[ayT-1 +(1 -
3. Teoretyczne podstawy programu3.4. Metoda Glauerta Rozwiązanie równania 3.3.16 sprowadza się do
Transport�7 według tych wymiarów otrzymuje się R = 350 cm, Fv = 240 em?, 7j, -- 15 881 cm4, ei = 28,
16155 PrepOrg II178 (2) 181 otrzymuje się 11,0 g (82,7?; ilości teoretycznej) bezbarwnego osodu o t.
więcej podobnych podstron