91410

pod kątem a. Zgodnie z prawem Hooke'a : a = x/G. Dolna powierzchnia rurki zostanie tym samym skręcona w stosunku do górnej o kąt cp.

(Powstanie tego skręcenia może nam ułatwić rysunek 10.7b. Ciało, narysowane przed ścinaniem linią ciągłą a po - linią przerywaną, wyobraźmy sobie jako cienką płytkę, powstałą z przecięcia rurki wzdłuż tworzącej i rozwiniętą na płaszczyznę. Zwińmy ją z pow-rotem w rurkę.) 5 = BB^f oznacza na rysunku 12.1 luk odpowiadający skręceniu o <p i równocześnie ścięciu o a. Dla małych wartości ar <p mamy a = s/l oraz (p = s! p skąd po wyeliminowaniu ^ otrzymujemy

(pp

a = — .

I

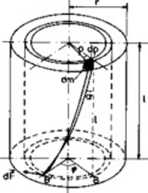
Rys. 111. Skręcenie jako skutek odkształcenia ścinającego

Podstawiając (12.1) oraz (12.2) do prawa Hooke'a (10.7) można otrzymać wyrażenie na silę df Ti p¹dpG<p ^dF=—j—>

a stąd, po pomnożeniu przez urn, moment siły dM.ldFp 2nG<p ₃

dkl.—y^p dp .

Całkowity moment siły działający na cały pręt otrzymamy całkując (12.4) w granicach (0, r)

Tl Gr‘

~~2T

M.

(12.5)

Indeks r przypomina, że jest to moment sil zewnętrzny cli, przyłożonych do pręta Jemu przeciwdziała równy co do wartości i kierunku (wzdłuż osi pręta) lecz przeciwny co zwrotu moment wewnętrznych sil sprężystości. Tak więc dla momentu sil sprężystych, jako skutku skręcenia pręta o kąt (p mamy ostatecznie

2