95719

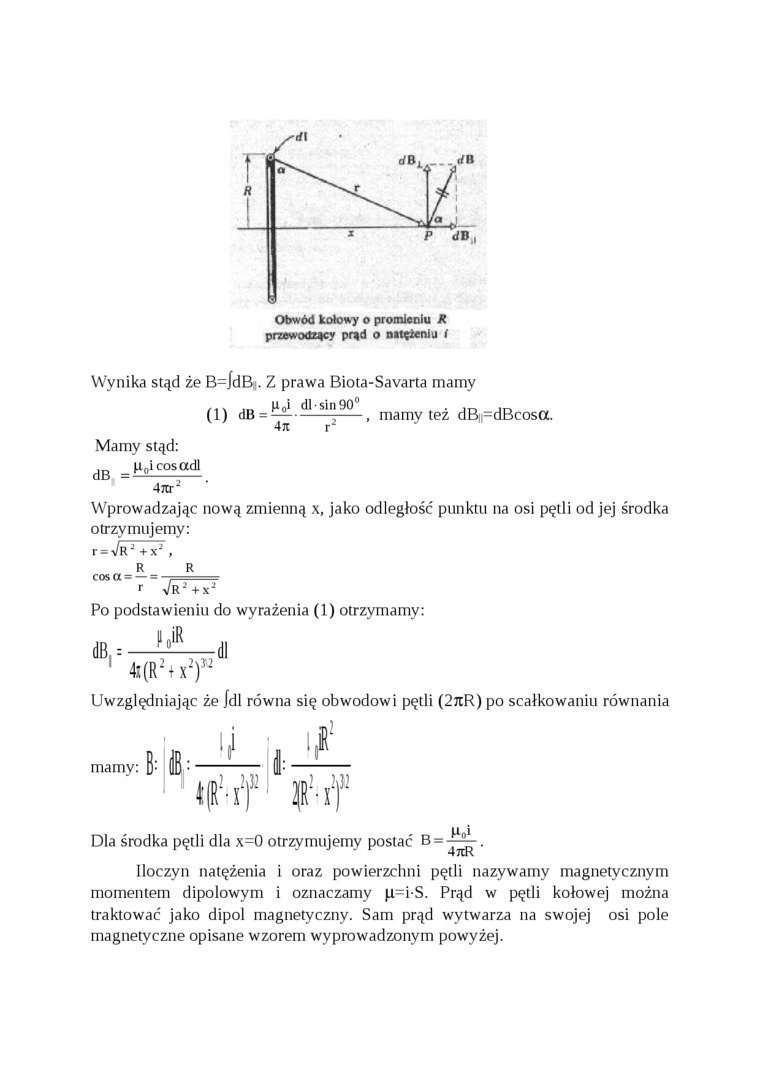
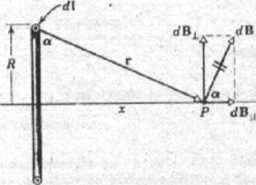
Obwód kołowy o promieniu R przewodzący prąd o natężeniu i

Wynika stąd że B=fdBj. Z prawa Biota-Savarta mamy p₀i dl sin 90°

(1) dB =

4jt r

mamy też dBpdBcosa.

Mamy stąd:

dB

p₀icosadl

4jtr²

Wprowadzając nową zmienną x, jako odległość punktu na osi pętli od jej środka otrzymujemy:

r = >/R² +x² ,

R R

cos a = — =

r VR²+x²

Po podstawieniu do wyrażenia (1) otrzymamy:

dB,: ‘‘/ ■dl

4:(R- + x)

Uwzględniając że Jdl równa się obwodowi pętli (2tcR) po scałkowaniu równania

mamy:

i-

ł(R‘-if

Dla środka pętli dla x=0 otrzymujemy postać B = -^- .

4 TIK

Iloczyn natężenia i oraz powierzchni pętli nazywamy magnetycznym momentem dipolowym i oznaczamy p=i-S. Prąd w pętli kołowej można traktować jako dipol magnetyczny. Sam prąd wytwarza na swojej osi pole magnetyczne opisane wzorem wyprowadzonym powyżej.