3360446720

a)

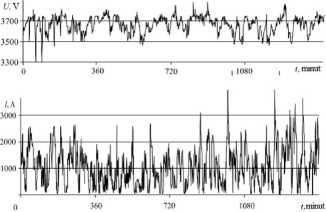
Fig. 1 - Time dcpendcnces of rectified feeder voltage (a) and current (b)

||a_ł.(t = 0) + /h5Jx yx[^_/(T = 0) + m_/²]

According to this theory, autocorrelation function of voltage u(t), as a stationary ergodic random process, it is possible to write down as the expectation of scalar work of the centring random

function U(t) and it’s shifted for the interval of correlation T of the copy U(t + T):

*r„(i)=M^(()-u(t+T)j=    ₍₂₎

where m_v - expectation of stationary random function ofvoltage U(t) (constant).

Similarly, the autocorrelation function E,(t) of random function of current E, (t) is:

*,(r)=jWp(/)./(!+r)]=    ₍₃₎

where rttj - expectation of stationaiy random function ofvoltage /(/) (constant).

For stationaiy' random processes in very wide terms [2], the unbiased estimate of expectation / [X(/)] of any stationary function X(/) is proved to be its mean value by time x of realization by the duration T of the function .¥(/), that’s

- 1 ⁷

«[*(()]=», = =    (4)

Then, in accordance with (4), expressions (2) and (3) for correlation functions can be written as:

K_u(x) = j\\U(t)-m_u\p(t+x)-m_u}it =

j\U(t)U(t + t)dt-    (5)

1 T    . T

-—|f/(r) ■m_udt -—J(/(r+t) m_vdt + ml, Similarly,

¹ T

, T    . T

-—J7(f) m,dt -—J/(f+t) m,dt + m). (6)

The autocorrelation function determines the law, characteristic of only one process (u(t) or ’(/)) and is used to fmd effective values of sizes. Indeed, at T = 0 expressions (5) and (6) are:

Kv (I = 0) J )/^! (O - ml ]= U’ - ml. (7)

K, (t = 0) = i j [/' (() - ml ]= /' - mi. (8)

where U and I - effective values of voltage and current, found with temporary realizations with the duration Ó.

Taking into account (7) and (8), total power is determined by autocorrelation function as

(9)

POJAZDY SZYNOWE NR 3/2011

14