3784502858

Poniższa tabela podaje orientacyjne ciśnienie atmosferyczne w funkcji wysokości nad poziomem morza.

Wysokość [mj Ciśnienie |hPa]

0	1013,25
500	954,61
1000	898,76
1500	845,58
2000	794,98
2500	746,86
3000	701,12
3500	657,68
4000	616,45
4500	577,33
5000	540,25
6000	471,87
7000	410,66
8000	356,06
9000	307,48
10000	264,42
11000	226,37

Przykład

Gdańsk Rabka-Zdrój Kuźnice (Zakopane) Pilsko, schronisko "Murowaniec' Kasprowy Wierch Rysy Zugspitze Lhasa Piz Bernina Matterhorn Ararat

Kilimandżaro Aconcagua Sziszapangma Mount Everest samoloty (FL 330) samoloty (FL 360)

Moduł ściśliwości

W dotychczasowych rozważaniach na temat płynów przyjmowaliśmy, że są one nieściśliwe. Obecnie spróbujemy zastanowić się, jak dokładne czy też niedokładne jest to założenie. Sztabka ciała stałego ściśnięta przez przyłożone na jej końcach siły wykazuje względną zmianę długości proporcjonalną do siły działającej na jednostkę powierzchni. Podobnie, jeżeli poddamy materiał działaniu skierowanych dojego wnętrza jednolitych sił, tojego objętość zmaleje. Oporność materiału na odkształcenia tego typu charakteryzuje moduł ściśliwości K. Jak się wkrótce przekonamy, zmiany objętości, a co za tym idzie gęstości

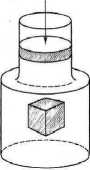
cieczy są w większości przypadków bardzo małe i na ogół mogą być pominięte.

Rys. Sposób przykładania sił zewnętrznych działających na całą powierzchnię ciała stałego

AK    Znaki występujące w tym równaniu

^ ~ ~^K~y ⁼ Kobrazująfakt, że wzrost ciśnienia powoduje wzrost gęstości, ale

zmniejszenie objętości. Moduł ściśliwości K ma zawsze wartość dodatnią. W tab. poniżej podano wartości współczynnika K dla pewnych ciał stałych i cieczy. Poniższy, przejaskrawiony przykład, obrazuje, jak niewielkie są zmiany objętości i gęstości spowodowane ściskaniem dla ciał stałych i cieczy.