3784503827

PRZEGLĄD GÓRNICZY 2010

PRZEGLĄD GÓRNICZY 2010

fcaupnstałuo*

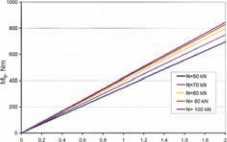
Rys. 4. Zależność maksymalnej wartości momentu zginającego działającego na śrubę od wartości kąta przekosu dla różnych w artości osiowej siły rozciągającej śrubę

Stałe całkowania wyznaczamy z warunków brzegowych. Dla współrzędnej x =0 ugięcie osi śruby wynosi: y = 0. Korzystając z równania (3) wyznaczamy stałą C:

Dla współrzędnej x =0 kąt ugięcia osi śruby wynosi:^ = 0 =>korzystając z równania (4) wyznaczamy stałą D

A

Podstawiając wyznaczone stałe całkowania do równań (3) i (4) otrzymamy ogólne równania na linię i kąty ugięcia osi śruby:

— (£-x)tga + /

A-tgA AL

fV_g A tg h AL

z' =(-+ Z,tga -/)Asin/rAx-

N-cosa

-    (A cos/i Ax + tga)

A

W celu wyznaczenia zależności pomiędzy' maksymalnym ugięciem osi śruby a wartościami siły osiowej N i momentu zginającego M, skorzystamy z warunku, iż w punkcie B ugięcie wynosi / .

Dla x = L,z = f oraz korzystając z równania (5) wyznaczamy f.

->    (7)

Z kolejnego warunku brzegowego wynika że: dla x = L,i - tg a oraz. korzystając z równania na kąty' ugięcia osi śruby (6) otrzymamy:

M

tga =(-+ Z, tga -/)Asin/r AZ,-

Ał-cosa

- ^-(A cos h AL + tga) A

Uw zględniając w równaniu (8) zależność (7) wyznaczymy wartość momentu zginającegow funkcji siły podłużnej N oraz kąta «:

Al sina

M =- ₍o\

A sinA AL

Maksymalny moment zginający' będzie działał na śrubę w punkcie A. Jego wartość obliczamy z zależności (1):

M_gmK = M+N(L sin a -/cos a)    (10)

Podstawiając do rów nania (10) zależności (7) i (9) otrzymamy równanie na maksymalną wartość momentu zginającego działającego na śrubę w zależności od siły' podłużnej:

(U)

Na ry sunku 4 przedstawiono wynikające z równania (11) zależności pomiędzy wartościami maksymalnego momentu zginającego działającego na śrubę a w artościami kąta przekosu a dla różnych wartości siły podłużnej AZ

Analizując wykresy przedstawione na rysunku 4 należy stwierdzić, że decydujący wpływ na wartość momentu zginającego działającego na śnrbę ma w artość kąta przekosu a. Wzrost wartości siły rozciągającej śrubę wpływa w znacznie mniejszy m stopniu na wartość momentu zginającego. Należy oczywiście mieć na uwadze fakt, że są to, szczególnie dla kątów powyżej jednego stopnia, obliczenia nie uwzględniające odkształceń plastycznych śruby.

Moment zginający powoduje pow stawanie w przekroju poprzecznym śruby naprężeń zginających, których wartość możemy wyznaczy ć z zależności

_^M«max

°^s~~irT

Siła podłużna N wywołuje w przekroju poprzecznym śruby naprężenia normalne (rozciągające), które wyznaczamy z zależności

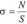
gdzie S przekrój poprzeczny rdzenia śruby

Wyznaczając z tych rów nań M_g)m i N i podstaw iając do równania (11) wyznaczymy wartości naprężeń zginający ch w funkcji naprężeń rozciągających śrubę

(12)

Podstawiając do równania (12) parametry' dla śruby M24 [5] wyznaczamy zależności pomiędzy naprężeniami zginającymi a naprężeniami rozciągającymi w śrubie (rys. 5).

Analiza wykresów z rysunku 5 wskazuje, że im większy jest kąt przekosu, ty m bardziej w zrasta udział naprężeń zginających w^f stosunku do naprężeń rozciągających w śrubie. Dla niskich wartości tego kąta (do około 0.5°) udział naprężeń zginających jest mniejszy' od naprężeń rozciągających. Dla wyższy ch w artości kąta w idoczny jest duży w zrost naprężeń zginających. Wzrost wartości osiow ej siły rozciągającej A' powoduje zmniejszenie udziału naprężeń zginających, a wzrost naprężeń rozciągających.

Korzystając z równania (11) można wyznaczyć zależności pomiędzy naprężeniami zginającymi i rozciągającymi a stosunkiem długości odcinka zginanego śruby do średnicy jej rdzenia (jest to tzw. elastyczność śmby). Równanie (11) po przekształceniach będzie miało następującą postać: