3826200191

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego LISTA 9 - Ruch drgający i fale

9.1    Równanie ruchu punktu dane jest w postaci: x(t)=sin(0,67zt). Znaleźć te chwile, w których występuje maksymalna prędkość i maksymalne przyśpieszenie.

9.2    Energia całkowita ciała drgającego harmonicznie jest równa E_c a maksymalna siła działająca na ciało F_max. Napisać równanie ruchu tego ciała, jeśli okres drgań trwa T a faza początkowa wynosi cp_Q.

9.3    Na gumce o długości L i promieniu R wisi odważnik o masie M . Wiedząc, że moduł Younga tej gumy wynosi E, znaleźć okres T pionowych drgań odważnika.

9.4    Areometr o masie m pływa w cieczy. Gdy zanurzy się go w cieczy i puści, zaczyna wykonywać drgania z okresem T . Przyjmując, że drgania są nietłumione, znaleźć gęstość cieczy, w której pływa areometr. Średnica walcowej rurki areometru wynosi d .

9.5    Przez Ziemię przewiercono tunel. Do tunelu wpuszczono kulkę. Znaleźć czas potrzebny do osiągnięcia przez kulkę środka Ziemi, a także prędkość, z jaką kulka minie środek Ziemi.

9.6    Jak zmieni się okres drgań pionowych masy wiszącej na dwóch jednakowych sprężynach, gdy połączenie szeregowe sprężyn zostanie zastąpione połączeniem równoległym?

9.7    Drgania zadane są równaniem x(t)= A(t)-sin(2;zfjt), gdzie amplituda zmienia się w czasie zgodnie z zależnością A(t)= Ąj(l + cos^^O) • Znaleźć składowe harmoniczne tych drgań.

9.8    Okres drgań tłumionych jest równy T, dekrement tłumienia A, a faza początkowa wynosi zero. Wychylenie punktu w chwili t = 0,25T jest równe x,. Napisz równanie ruchu tych drgań.

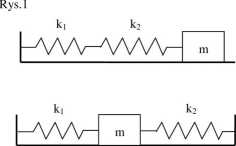
9.9    Masa m jest przyczepiona do dwóch sprężyn o stałych sprężystości k, i k,(Rys.l). W obu przypadkach zostaje ona wychylona z położenia równowagi i puszczona; porusza się bez tarcia. Obliczyć okres ruchu harmonicznego w obu przypadkach.

9.10    Równanie    wymuszonych    drgań:    x(t) = A- cos(Qt + <f>),

gdzie A=F/_A/m²(p² -co²)+ p²Cl² . Amplitudy drgań wymuszonych odbywających się pod działaniem dwóch sił zewnętrznych o częstościach kołowych <y, i o)₂ są równe. Wyznaczyć częstość rezonansową Q_rez.

14