3826200312

12

Rozdział 2. Modele matematyczne silników prądu stałego

przy czym:

x,(t) =

»«(*) 1

<*»(*) J ’

“.(*) 1

M₀(t) \

(2.14)

jest wektorem stanu a u_SUI wektorem wymuszeń. Macierze stanu (A_s) i wymuszeń (B_sw) są następujące:

A_s =

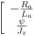
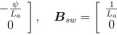
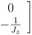
(2.15)

2.3. Model silnika prądu stałego w dziedzinie operatorowej

Można także zapisać model matematyczny silnika wykorzystując przekształcenie Łapiące^. Układ równań 2.12 po przekształceniach przyjmie postać:

siat⁸) =    + J-ti„(s)    (2.16)

sw_m(s) = jia(s) - 2-Mo(s)

Dokonując prostych przekształceń można zapisać równania w postaci, gdzie w sposób jawny wyodrębnione będą podstawowe człony dynamiczne takie jak: człon proporcjonalny, człon całkujący i człon inercyjny pierwszego rzędu.

i_a(s) = [u_a{s) - ił>u_m(s)]^

v_m(s) = [ipi_a(s) - M₀(s)]-^~    (2.17)

Wprowadzając pojęcie stałej czasowej obwodu T_e = j*-, równania 2.17 można zapisać w równoważnej postaci:

i

(„W = K(S) -

<4_m(s) = [V>i„(s)-M₀(s)]-i-    (2.18)

Bazując na zależnościach (2.18) można przedstawić model silnika prądu stałego w postaci graficznej prezentowanej na rys. 2.3.

2.4. Model matematyczny przekształtnika energoelektronicznego

Właściwości dynamiczne przekształtnika tyrystorowy lub tranzystorowego można aprok-symować wprowadzjąc człon z opóźnieniem, u_a(t) — ku_s(t — T_p) którego transmitancja ma postać: