3826200314

14

Rozdział 2. Modele matematyczne silników prądu stałego

Wprowadzając pojęcie wektora stanu, wektora wymuszeń i odpowiednio macierzy stany i macierzy wymuszeń można zapisać model matematyczny silnika prądu stałego i przekształtnika energoelektronicznego w postaci macierzowego równania stanu:

u(t) ■ “m(f) U_a(t)

u,(t) 1 M.(t) \

x,p(t) = U_v(t) =

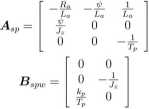
^ x,_p(t) — A_SpXsp(t) -I- Bapu/Uppit)

(2.23)

(2.24)

(2.25)

(2.26) (2.27)

Jeśli wykorzystujemy opis matematyczny do projektowania regulatorów to wskazane jest zmodyfikowanie równań (2.13) wprowadzając równoważny zapis po dokonaniu rozdzielenia wektora wymuszeń na wektor sygnałów sterujących i wektor sygnałów zakłóceń:

(f) = A_epXgp(t) + B_vu,_r(t) + E_vz._p(t)    (2.28)

przy czym wektory sterowań i zakłóceń oraz macierze sterowań i zakłóceń przyjmują postać:

(2.29)

u_sp(t) — [w_s(i)] > ^zsp(t) — [M₀(t)\

	0		0
B,„ =	0 7^	i ESp =	~Tz 0

(2.30)

W celu dokładniejszego opisu zjawisk w układzie napędowym wprowadza się uzupełnienie części mechanicznej modelowanego silnika o model tarcia. Dla uproszczenia można przyjąć, że uwzględnione będzie tylko zjawisko tarcia ślizgowego. Moment oporowy związany ze zjawiskiem tarcia ślizgowego jest proporcjonalny do prędkości kątowej wirnika.

M_ts — Ct&m

(2.31)

Rozszerzony opis matematyczny przekształtnika i silnika z uwzględnieniem tarcia jest dany równaniami:

(2.32)

^•Esp(^) — A_:ipiXsp{t') + B_spwUsp(t)

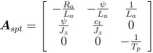
(2.33)

gdzie

- Ct - współczynnik tarcia ślizgowego