9142891021

podstawiając:

s_c+s, =w„,

:otrzymamy:

M_R=W_pl-f_d

gdzie:

S_c, Si -odpowiednio moment statyczny strefy ściskanej i rozciąganej przekroju,

W_pi - plastyczny wskaźnik wytrzymałości

Dlatego też znając współczynnik rezerwy plastycznej przekroju a_pi można obliczyć nośność przekroju w stanie plastycznym, przemnażając nośność w stanie sprężystym przez ten współczynnik: .

M_R=a_pl-W_x-f_d

Przykładowo wartość współczynnika rezerwy plasty cznej przekroju a_pi dla belki o przekroju prostokątnym oblicza się następująco:

b

x

i

W_x

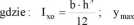
h

2

▼

W„ =    • =

12 h 6

y„

rys.1.13

natomiast

h h² -b

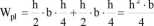
zatem współczynnik a_pi dla tego przekroju jest równy:

AlmaMater