6830718986

Równanie Bernoulliego dla płynów rzeczywistych

Jeśli wykonać urządzenie pokazane na poniższym rysunku, to przy przepływie cieczy rzeczywistej obserwuje się różny poziom cieczy w rurkach spiętrzających wzdłuż jej przepływu. Jest to wynikiem straty ciśnienia spowodowaną tarciem płynu o ściany rury.

Dla takiego przypadku równanie Bernoulliego dla przekrojów 1 i 2 przyjmuje postać:

,    w,² p    , Wjp ,

Pi + P g hi h = p₂ + p g h₂ h + Ap_glnt

Stratę ciśnienia obserwuje się nie tylko podczas przepływu przez rurociągi proste, ale także przez różne elementy aparatury, w których następuje jakakolwiek zmiana kierunku przepływu płynu są to wtedy tak zwane opory miejscowe.

Stratę ciśnienia na prostych odcinkach rurociągów oblicza się z równania Darcy-Weisbacha:

Ap_a

L w²

A--p

d 2 ^M

Wartość współczynnika oporu przepływu zmienia się wraz z liczbą Reynoldsa:

64

Dla ruchu laminarnego: X = —

Dla ruchu burzliwego wzór Blasiusa: X =

Te zależności funkcyjne są wyznaczone doświadczalnie i w literaturze można spotkać także inne równania, lub zależności graficzne.

Jeśli przewód, którym płynie płyn nie ma przekroju kołowego, to w liczbie Reynoldsa, w miejsce średnicy, należy wstawić zastępczy wymiar liniowy. Zastępcza średnica hydrauliczna obliczana jest jako iloczyn czterech promieni hydraulicznych definiowanych:

A

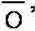
zatem

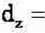
4 A O

Przykładowo dla przestrzeni międzyrurowej w wymienniku ciepła typu rura w rurze o średnicach D oraz d:

1