CCF20120509001

tzęsc i. rr/yKiaay i zauuma

<\L

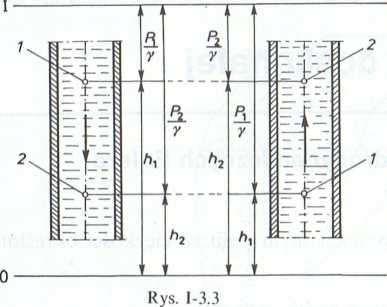
3.1.4. (Rys. 1-3.3). Wyprowadzić równanie Bernoulliego dla ustalonego przepływu cieczy doskonałej przez przewód pionowy o stałym przekroju. Rozważyć przypadek ruchu cieczy z góry w dół oraz z dołu w górę.

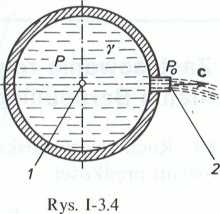
3.1.5.    (Rys. 1-3.4). W zamkniętym zbiorniku znajduje się ciecz doskonała pod ciśnieniem absolutnym p > p_u. Oblicz prędkość wypływu cieczy zakładając, że ciśnienie wewnątrz zbiornika nie ulega zmianie. Wszelkie straty pominąć.

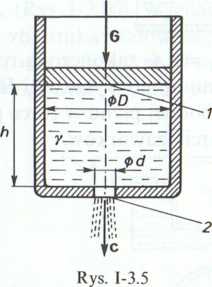
3.1.6.    (Rys. 1-3.5). W dnie naczynia cylindrycznego o średnicy D znajduje się otwór, którego średnica jest równa d. Nad cieczą wypełniającą naczynie umieszczono tłok o ciężarze G, poruszający się szczelnie, lecz bez tarcia. Pomijając straty w otworze wypływowym, określić zależność pomiędzy prędkością c₂ wypływającej cieczy, a położeniem h tłoka. Przyjąć ciężar właściwy cieczy równy y.

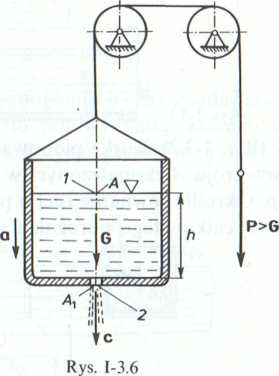
3.1.7. (Rys. 1-3.6). Zbiornik, którego ciężar wraz z zawartą w nim cieczą wynosi Oj porusza się w górę pod działaniem siły ciężkości P > G. Pomijając straty w otworze wypływowym oraz tarcie w krążkach, obliczyć prędkość wypływu cieczy ze zbiornika w chwili, gdy wysokość słupa cieczy jest równa h.

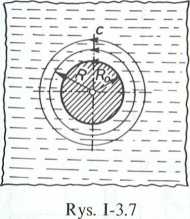
.U .8. (Rys. 1-3.7). Określić rozkład ciśnienia cieczy doskonałej w funkcji promienia (i l(R), w płaskim stacjonarnym przepływie kołowosymetrycznym, wokół walca • * promieniu R„. Rozkład prędkości cieczy opisuje zależność c = k/R, w której k jest »trik ością stałą. Pominąć wpływ siły ciężkości oraz przyjąć, że ciśnienie na ściance o ulen jest równe p₀, a gęstość cieczy wynosi p.

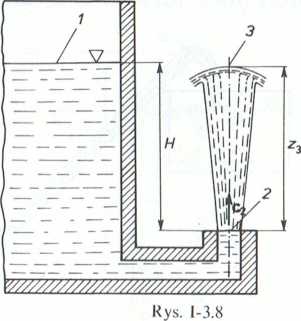
3.1.9. (Rys. 1-3.8). W dużym otwartym zbiorniku znajduje się ciecz doskonała, i- riijąca wolnym zwierciadłem nad otworem wypływowym na wysokość H = const. Wyznaczyć prędkość średnią c₂ w przekroju 2 oraz wysokość z₃, na jaką podniesie się lllimień cieczy wypływającej ze zbiornika.

U. 10. (Rys. 1-3.9). Dwa duże zbiorniki wodne o różnicy poziomów cieczy równej il zostały połączone przewodem w sposób przedstawiony na rysunku. Obliczyć piydkość c₂, z jaką woda wpływa do zbiornika dolnego. Przedstawić wykreślnie iilliiny energii potencjalnej, wewnętrznej (ciśnienia) i kinetycznej w odniesieniu do i’ ilnostkowej masy cieczy.

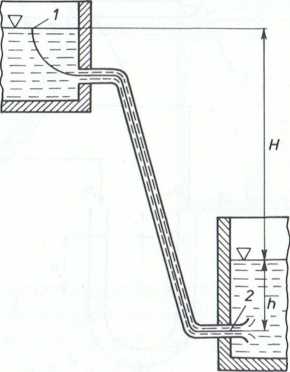
Rys. 1-3.9