CCF20120509022

i>4 tzęsc i. rr/yKiaay i zadania

i>4 tzęsc i. rr/yKiaay i zadania

			T 1
	7/7	77 0	fV//// D			777777777/

b)

		-h j				CJ			—r i |
7777	1777777777777 00				7 ’ 7/7	777777	77	7/7	w

Rys. 1-5.31

5.4.3.    Czy oderwanie warstwy przyściennej nastąpi podczas ruchu:

a)    przyspieszonego,

b)    jednostajnego,

c)    opóźnionego?

5.4.4.    Dlaczego statyczne sondy pomiarowe reagują bardzo czule na zmianę kierunku napływającej cieczy lub gazu?

5.4.5.    (Rys. 1-5.32). Na rysunek 1-5.32 nanieść wykres ilustrujący zmianę Współczynnika ciśnienia

C_p(x)

2Q(x)-p₀₀]

pvi

od krawędzi natarcia, aż do punktu oderwania warstwy przyściennej.

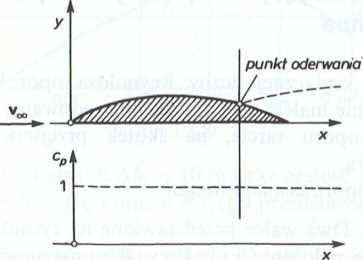
Rys. 1-5.32

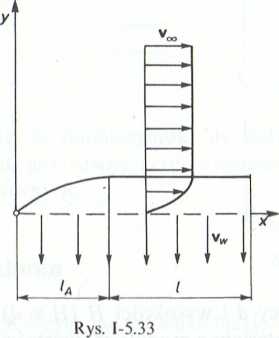
5.4.6. (Rys. 1-5.33). Jeżeli na płaskiej płycie, opływanej ze stałą prędkością t;^, wystąpi odsysanie z prędkością normalną v_w < 0, to za odcinkiem rozbiegowym l_A ustali się przepływ o stałej grubości warstwy przyściennej S. Wówczas dla x > l_A, prędkość i ciśnienie będą niezależne od x. Wyprowadzić równanie opisujące profil prędkości v(y)/v₀₀ = f(y), jaki utworzy się na odcinku /.

Rys. 1-5.34

5.4.7.    Samolot leci z prędkością v = 450 km/h w powietrzu, którego współczynnik lepkości kinematycznej v = 0,142• 10“⁴ m²-s^_1. Korzystając ze wzorów dla pły płaskich, obliczyć współczynnik oporu tarcia oraz grubość warstwy przyściennej m krawędzi spływu płata o cięciwie / = 2,40 m.

5.4.8.    Obliczyć opór tarcia gładkiej płyty o cięciwie / = 1 m i rozpiętości L=4m ustawionej równolegle do kierunku przepływającej wody, której gęstośi p = 1000 kgm“³, a współczynnik lepkości kinematycznej v = 1,00 -10“⁶ m²-s“ (T = 293 K). Zadanie rozwiązać, przyjmując prędkość wody równą:

a)    = 1 m-s^-1,

b)    v_x — 20 m • s ¹.

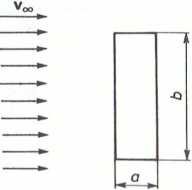
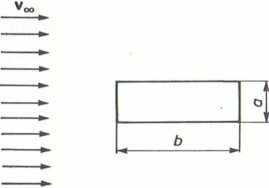
5.4.9.    (Rys. 1-5.34). Gładką płytę o wymiarach a x b = 0,5 x 2 m wstawiom krótszym, a następnie dłuższym bokiem, równolegle do kierunku prędkości prze pływającej wody. Obliczyć dla tych dwóch położeń stosunek oporów tarcia, jeżel współczynnik lepkości kinematycznej wody (w temperaturze T = 293 K) wynos v = 1 • 10“⁶ m² s^_1, a prędkość strumienia niezakłóconego v_m = lOm-s"¹.

5.4.10.    Nafta o kinematycznym współczynniku lepkości v = 12-10“⁶ m²-s“

i gęstości p = 810 kg-m ³ (przy 7= 283 K) opływa gładką nieruchomą płytę