CCF20120509009

5N Częsc I. Przykłady i zadania

3.4.9. (Rys. 1-3.51). Określić objętościowe natężenie przepływu cieczy doskonałej przez przelew, którego przekrój jest półkolem o średnicy d.

5N Częsc I. Przykłady i zadania

Rys. 1-3.51

Rys. 1-3.52

3.4.10. (Rys. 1-3.52). Naczynie o ciężarze G i średnicy wewnętrznej D oparte jest symetrycznie na dwóch podporach pryzmatycznych A i B. W środku dna naczynia zamontowano króciec o średnicy d, zamykany zaworem. Obliczyć nacisk wywierany przez naczynie na podpory A i B, jeżeli zawór jest całkowicie otwarty. Pominąć straty i długość króćca oraz przyjąć wysokość poziomu cieczy w naczyniu równą h, a gęstość cieczy p.

3.4.11. (Rys. 1-3.53). Przez krzywak o zmiennym przekroju kołowym, usytuowany w płaszczyźnie poziomej, przepływa strumień cieczy doskonałej o natężeniu Q = 1800 m³/h. Kąt zagięcia krzywaka a = f, a średnice przekrojów — dopływowego i odpływowego — wynoszą: D = 600 mm i d = 400 mm. Wyznaczyć napór hydrodynamiczny R, jeżeli gęstość cieczy p = 1000 kg-m^-3, a ciśnienie w przekroju dopływowym krzywaka p_t = 200 kPa.

Rys. 1-3.53

Rys. 1-3.54

3.4.12. (Rys. 1-3.54). Na platformie, która porusza się bez tarcia, zamontowano zbiornik wypełniony do wysokości h = 1 m cieczą doskonałą o gęstości p = 1000 kg-m ³. Po dwóch przeciwległych stronach zbiornika znajdują się dwa jednakowe zawory, z otworami o powierzchni przekroju przepływowego A = 10 cm² każdy. Pierwszy z zaworów znajduje się na wysokości h_t = 0,25 m, a drugi na wysokości h₂ = 0,5 m od dna naczynia. Określić moduł, kierunek oraz zwrot siły R, którą należy zrównoważyć reakcje hydrodynamiczne, aby po otwarciu zaworów platforma pozostała w stanie spoczynku.

3.4.13. (Rys. 1-3.55). Strumień cieczy o przekroju poprzecznym A, płynący z prędkością c, działa na wklęsłą, ruchomą łopatkę w kształcie czaszy kulistej. Łopatka porusza się w tym samym kierunku co strumień główny cieczy. Wyznaczyć, dla jakiej prędkości u przemieszczania się czaszy moc składowej poziomej reakcji hydrodynamicznej będzie maksymalna?

Rys. 1-3.55

3.4.14. (Rys. 1-3.56). Przez wirnik turbiny wodnej, obracający się z prędkością kątową a> = 16 s¹, przepływa strumień wody o natężeniu Q = 0,1 m³-s~'. Średnica zewnętrzna wirnika D = 1800 mm, a wewnętrzna — d = 1500 mm. Obliczyć moc teoretyczną N oraz sprawność 77 turbiny, jeżeli kierunek wektora prędkości bezwzględnej c, = 30 m s^-1 na dopływie, tworzy kąt a = 0,16771 ze styczną do koła zewnętrznego wirnika, a kierunek wektora bezwzględnej prędkości wypływu c₂ = 4 m-s^-1, nachylony jest pod kątem /? = 0,47271 do stycznej koła wewnętrznego.

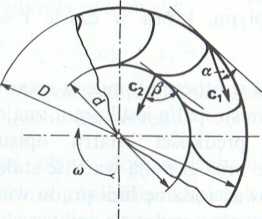
Rys. 1-3.56