CCF20120509�003
4<> Część I. Przykłady i zadania 3. Dynamika cieczy doskonałej 47
4<> Część I. Przykłady i zadania 3. Dynamika cieczy doskonałej 47
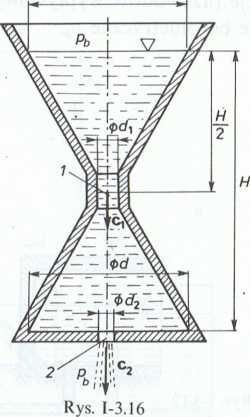
3.1.19. (Rys. 1-3.18). Określić minimalną wysokość H położenia zwierciadła w otwartym zbiorniku A, przy której woda przepływająca przez zwężkę będzie mogła zasysać ciecz (o takiej samej gęstości), znajdującą się w naczyniu B. Odległość pomiędzy poziomem cieczy w naczyniu dolnym a osią zwężki wynosi li = 4m, Średnice zwężki przyjąć, odpowiednio, d = 300 mm i d{ = 200 mm. Straty przepływu pominąć oraz założyć, że ciśnienie na powierzchniach swobodnych w zbiornikach A i B i w przekroju wypływowym jest równe ciśnieniu barometrycznemu ph.
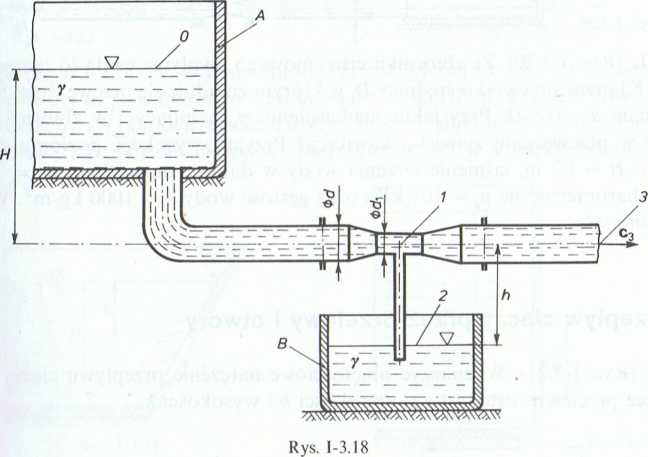
3.1.16. (Rys. 1-3.15). Dwa sąsiadujące ze sobą zbiorniki mają w ścianach bocznych otwory o średnicach d, i d2. Wiedząc, że różnica poziomów wody w zbiornikach jesl stała i wynosi H = 1 m, a głębokość zanurzenia otworu o średnicy d2 jest równa H{ = 1,5 m, obliczyć prędkości wypływu cieczy c2 i c3 oraz stosunek średnic djd2 Straty w otworach pominąć.
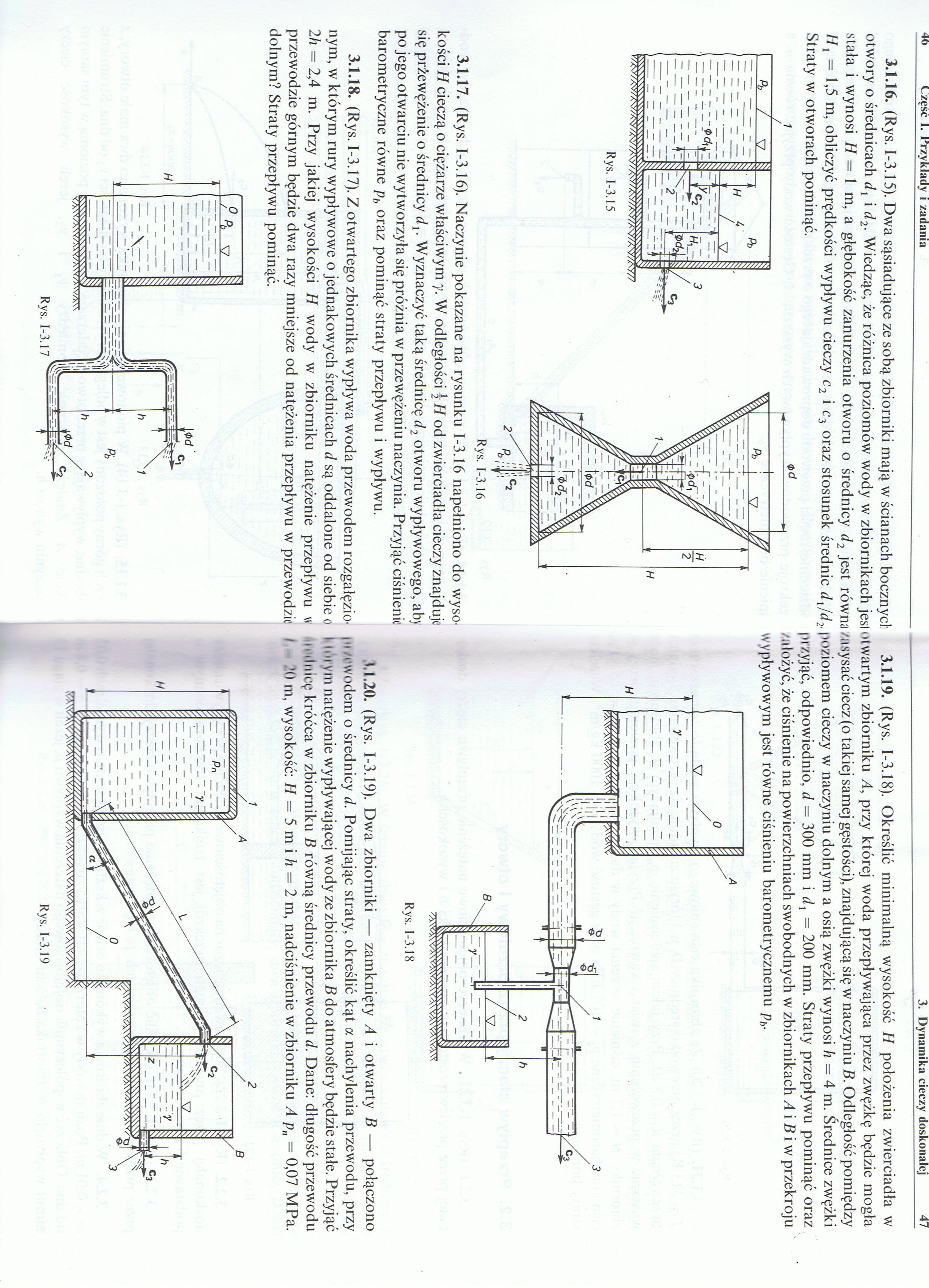
3.1.17. (Rys. 1-3.16). Naczynie pokazane na rysunku 1-3.16 napełniono do wysokości H cieczą o ciężarze właściwym y. W odległości \ H od zwierciadła cieczy znajduje się przewężenie o średnicy <7,. Wyznaczyć taką średnicę d2 otworu wypływowego, aby po jego otwarciu nie wytworzyła się próżnia w przewężeniu naczynia. Przyjąć ciśnienie barometryczne równe ph oraz pominąć straty przepływu i wypływu.
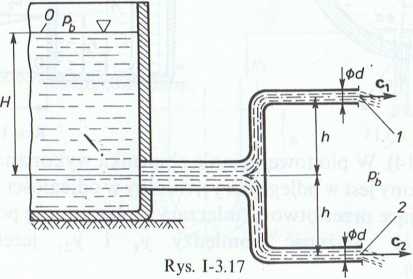
3.1.18. (Rys. 1-3.17). Z otwartego zbiornika wypływa woda przewodem rozgałęzionym, w którym rury wypływowe o jednakowych średnicach d są oddalone od siebie o 2/j = 2,4 m. Przy jakiej wysokości H wody w zbiorniku natężenie przepływu w przewodzie górnym będzie dwa razy mniejsze od natężenia przepływu w przewodzie dolnym? Straty przepływu pominąć.
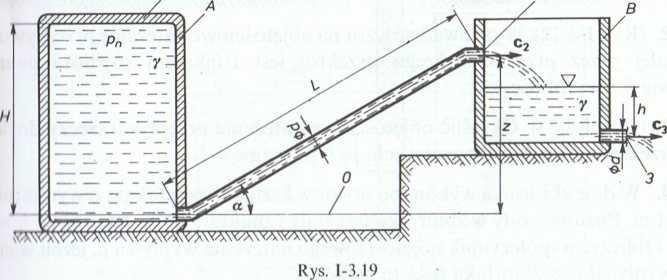
3.1.20. (Rys. 1-3.19). Dwa zbiorniki — zamknięty A i otwarty B — połączono 1'i/t'wodem o średnicy d. Pomijając straty, określić kąt a nachylenia przewodu, przy Mól vu) natężenie wypływającej wody ze zbiornika B do atmosfery będzie stałe. Przyjąć i. .lnicę króćca w zbiorniku B równą średnicy przewodu d. Dane: długość przewodu l .’() ni, wysokość: H = 5 m i h = 2 m, nadciśnienie w zbiorniku A pn = 0,07 MPa.
1 2
Wyszukiwarka
Podobne podstrony:
CCF20120509�002 V,/,pt I. /•j Kłulij i /.auuiiia 3. Dynamika cieczy doskonalej 4t> V,/,
CCF20120509�031 Dynamika cieczy doskonałej Ruch cieczy doskonałej można ogólnie opisać zależnościami
Mechanika@9 £ Przykład. (Zadanieodwrotne dynamild) Ciało o masie m porusza się po
CCF20120509�008 ( zęść I. Przykłady i zadania 3.4.2. (Rys. 1-3.44). Otwarty zbiornik wypełniono wodą
CCF20120509�012 Część I. Przykłady i zadania 4.3.4. (Rys. 1-4.4). Na powierzchni swobodnej cieczy do
CCF20120509�009 5N Częsc I. Przykłady i zadania 3.4.9. (Rys. 1-3.51). Określić objętościowe natężeni
CCF20120509�019 7H Część 1. Przykłady i zadania cieczy w zbiorniku, aby objętościowe natężenie wypły
CCF20120509�023 HO Część l. Przykłady i zadania wstawioną równolegle do kierunku przepływu. Prędkość
CCF20120509�005 Część I. Przykłady i zadania kowicie zatopiony. Różnica wysokości poziomów niwelacyj
CCF20120509�006 52 Część 1. Przykłady i zadania 52 Część 1. Przykłady i zadania 3.3.7. (Rys. 1-3.33)
CCF20120509�007 54 Część I. Przykłady i zadania 3.3.14. (Rys. 1-3.40). W naczyniu cylindrycznym o pr
CCF20120509�011 62 Część I. Przykłady i zadania4.2. Ruch potencjalny płynu — zastosowanie rachunku z
CCF20120509�013 Część I. Przykłady i zadania 66 4.4.3. (Rys. 1-4.10). Płaski przepływ przez dyszę mo
CCF20120509�014 <>N Część 1. Przykłady i zadania Wyznaczyć: a) pole wektorow
CCF20120509�020 KO Częsc I. Przykłady i zadania oraz zakładając, że końce B, C i D przewodów znajduj
CCF20120509�021 (z Część I. Przykłady i zadania 5.3.4. (Rys. 1-5.28). Prasę hydrauliczną o nacisku P
CCF20120509�025 vu częsc l. Przykłady i zadania CTzzzrzzzzzzzzzzzz p w 4 s V
więcej podobnych podstron