CCF20120509013

Część I. Przykłady i zadania

66

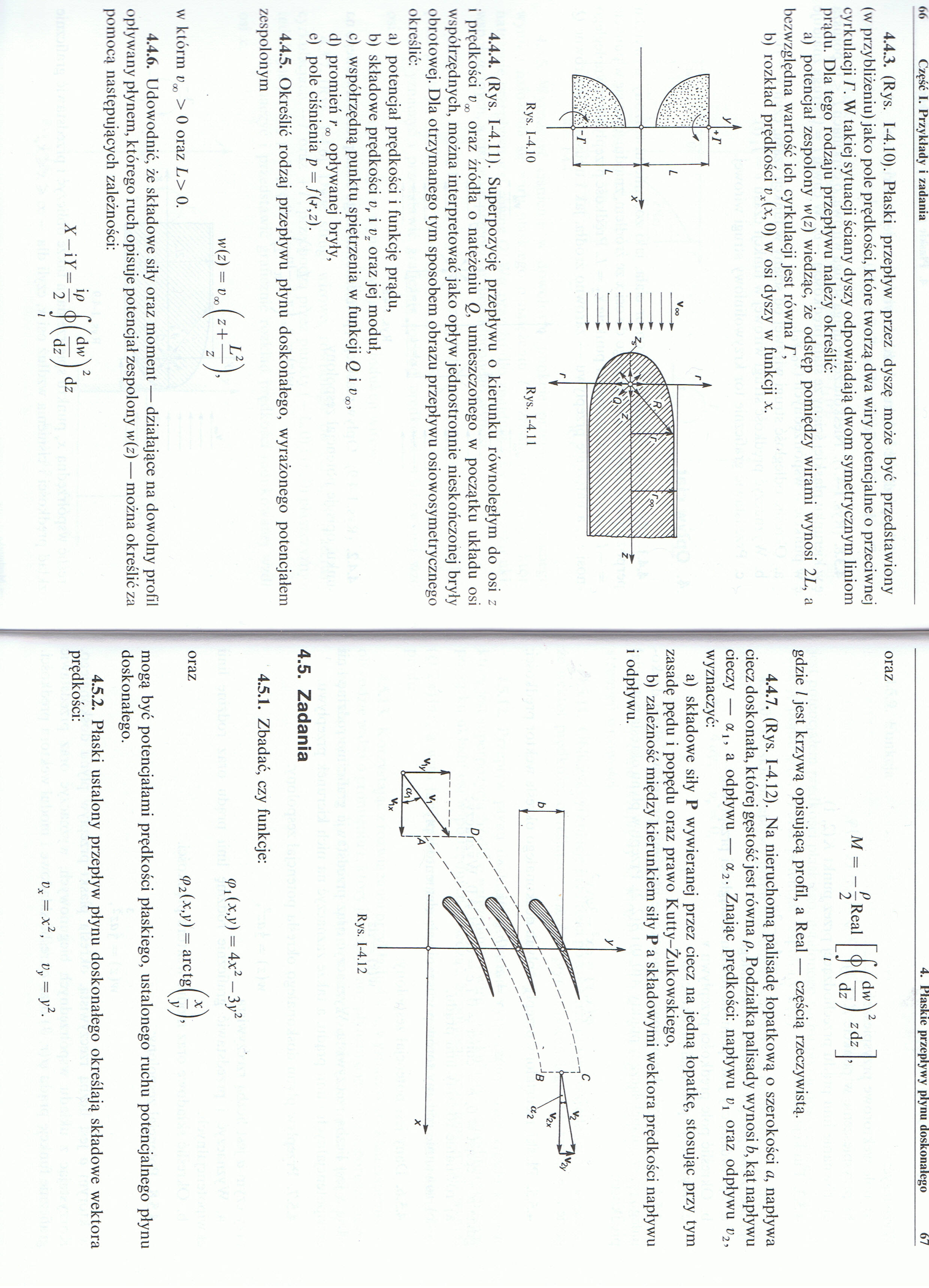
4.4.3. (Rys. 1-4.10). Płaski przepływ przez dyszę może być przedstawiony (w przybliżeniu) jako pole prędkości, które tworzą dwa wiry potencjalne o przeciwnej cyrkulacji r. W takiej sytuacji ściany dyszy odpowiadają dwom symetrycznym liniom prądu. Dla tego rodzaju przepływu należy określić:

a)    potencjał zespolony w (z) wiedząc, że odstęp pomiędzy wirami wynosi 2 L, a bezwzględna wartość ich cyrkulacji jest równa T,

b)    rozkład prędkości v_x(x, 0) w osi dyszy w funkcji x.

Rys. 1-4.11

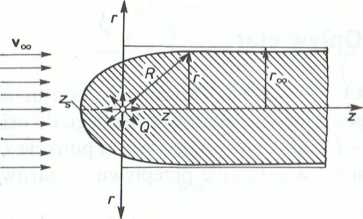
4.4.4. (Rys. 1-4.11). Superpozycję przepływu o kierunku równoległym do osi z i prędkości v_m oraz źródła o natężeniu Q, umieszczonego w początku układu osi współrzędnych, można interpretować jako opływ jednostronnie nieskończonej bryły obrotowej. Dla otrzymanego tym sposobem obrazu przepływu osiowosymetrycznego określić:

a)    potencjał prędkości i funkcję prądu,

b)    składowe prędkości v_r i v_z oraz jej moduł,

c)    współrzędną punktu spiętrzenia w funkcji Q i v_m,

d)    promień opływanej bryły,

e)    pole ciśnienia p =f(-r,z).

4.4.5. Określić rodzaj przepływu płynu doskonałego, wyrażonego potencjałem zespolonym

w(z)

L²

zĄ--

z w którm v_o0 > 0 oraz L> 0.

4.4.6. Udowodnić, że składowe siły oraz moment — działające na dowolny profil opływany płynem, którego ruch opisuje potencjał zespolony w (z) — można określić za pomocą następujących zależności:

X-i Y=

jP

2

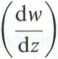
2

d z

/

M = — - Real 2

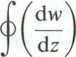
oraz

^dWY H 1

Tz)^zdz ’ gdzie / jest krzywą opisującą profil, a Real — częścią rzeczywistą.

4.4.7. (Rys. 1-4.12). Na nieruchomą palisadę łopatkową o szerokości a, napływa ciecz doskonała, której gęstość jest równa p. Podziałka palisady wynosi b, kąt napływu cieczy — a,, a odpływu — a₂. Znając prędkości: napływu v_t oraz odpływu v₂, wyznaczyć:

a)    składowe siły P wywieranej przez ciecz na jedną łopatkę, stosując przy tym zasadę pędu i popędu oraz prawo Kutty-Żukowskiego,

b)    zależność między kierunkiem siły P a składowymi wektora prędkości napływu i odpływu.

y

c

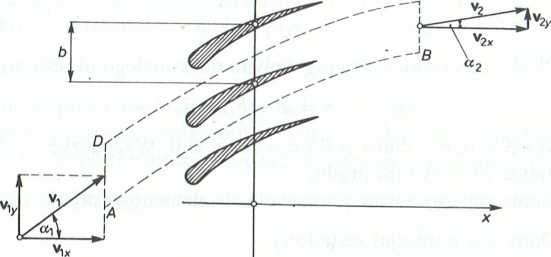
Rys. 1-4.12

4.5. Zadania

4.5.1. Zbadać, czy funkcje:

<Pi(^x’y) = 4x² — 3y²

^oraz    (p₂(^x-y) = arctg^Yj,

mogą być potencjałami prędkości płaskiego, ustalonego ruchu potencjalnego płynu doskonałego.

4.5.2. Płaski ustalony przepływ płynu doskonałego określają składowe wektora prędkości:

v.

= x², v_y = y².