CCF20120509012

Część I. Przykłady i zadania

4.3.4. (Rys. 1-4.4). Na powierzchni swobodnej cieczy doskonałej istnieje wir yisany potencjałem zespolonym w(z) = —iwlnz. Określić:

a)    prędkość v = f(r),

b)    równanie powierzchni swobodnej cieczy z* = fx(r),

c)    cyrkulację prędkości T.

z*'	y‘ T		r
\ ^0
		^1L	-J O

Rys. 1-4.4    ^Rys- '-⁴⁵

4.3.5.    Wyznaczyć ciśnienie w dowolnym punkcie przepływu otrzymanego w yniku nałożenia się wiru płaskiego o natężeniu T i źródła dodatniego, którego atężenie przepływu jest równe Q. Wir oraz źródło znajdują się w początku układu spółrzędnych, a ciśnienie przepływu niezakłóconego wynosi p_x.

4.3.6.    (Rys. 1-4.5). Dwie strugi wirowe, o jednakowej cyrkulacji T, przechodzi) rzez punkty ( — L,0) i (L,0) płaszczyzny x,y, indukując na niej pole prędkości.

a.    Wyznaczyć i przedstawić graficznie rozkład prędkości indukowanej wzdłuż

si x.

b.    Jaki ruch powstaje w wyniku wzajemnej indukcji wirów?

c.    Przedstawić graficznie obraz linii prądu.

4.3.7. (Rys. 1-4.6). Dwie strugi wirowe, równoległe do osi z, o przeciwnych yrkulacjach — T oraz + F, przechodzą przez punkty ( — L,0) i (L,0) płaszczyzny x,y, indukując na niej pole prędkości.

a. Wyznaczyć i przedstawić graficznie rozkład prędkości indukowanej wzdłuż

Rys. 1-4.7

y
-r	r
O	n
i	0 L x

Rys. 1-4.6

b.    Jaką prędkość indukuje każdy z wirów w miejscu drugiego?

c.    Przedstawić graficznie obraz linii prądu.

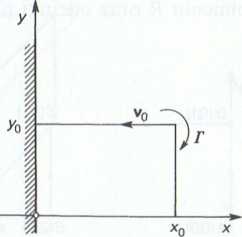
4.3.8. (Rys. 1-4.7). Nieskończenie długa struga wirowa, o cyrkulacji r < 0, porusza się w kierunku płaskiej ściany ze stałą prędkością —v₀. W chwili t = 0 struga znajduje się w punkcie o współrzędnych (x₀,y₀).

a.    Określić odległość strugi wirowej od ściany w funkcji czasu, czyli x =/(t).

b.    Wyznaczyć prędkość strugi wirowej w funkcji czasu v = j\ (t).

c.    Przedstawić graficznie tor krzywoliniowy strugi wirowej.

4.4. Opływ ciał

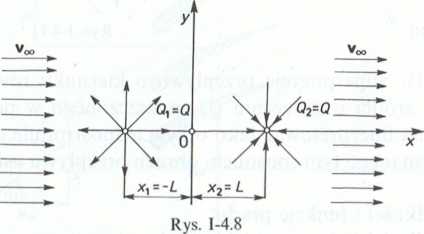
4.4.1. (Rys. 1-4.8). Wyznaczyć kontur ciała, jaki zostanie utworzony w wyniku superpozycji przepływu równoległego do osi x ze źródłem, znajdującym się w punkcie x₁ = —Li upustem, położonym w punkcie x₂ = L. Prędkość przepływu równoległego wynosi v₀₀, a natężenie przepływu — zarówno źródła, jak i upustu — jest równe Q.

4.4.2. (Rys. 1-4.9). Opływ płaskiego, półnieskończonego ciała, przedstawionego na rysunku, opisuje potencjał zespolony

w(z) = v₀₀[z + hn~_L).

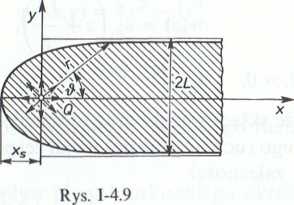
Określić współrzędną x_s punktu spiętrzenia, a także obliczyć i przedstawić graficznie rozkład prędkości i ciśnienia wzdłuż osi x, czyli dla — oo j$x<x_s.