CCF20120509019

7H Część 1. Przykłady i zadania

cieczy w zbiorniku, aby objętościowe natężenie wypływającej cieczy Q = 40 1-s ^x? Dane: h = 2 m, v = 1 • 10^-6 m²-s^-1, £_w = 0,5, £_t = 0,2, £_z = 5.

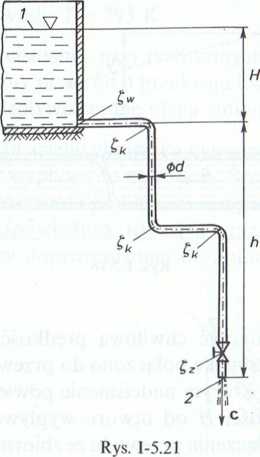
5.2.10. (Rys. 1-5.22). Przewodem o długości / = 100 m i średnicy d = 200 mm połączono otwarty zbiornik B ze zbiornikiem zamkniętym A. W zbiorniku A znajduje się paliwo pod ciśnieniem p_n = 0,08 MPa. Obliczyć minimalną średnicę D poszerzonej

>	fSkż-i			V
		§			h'
		■ -- r Łs. i oN	"—	-r-r-Bi

Rys. 1-5.22

końcówki rurociągu, przy której średnia prędkość paliwa, wpływającego do zbiornika B, nie przekroczy wartości c₂ = 1 m-s^-1. Dane: H_t = 9m, ł/₂ = 3m, gęstość paliwa p - 800 kg • m~ ³ oraz współczynniki strat: £_w = 0,5, (_d = 1, £_k = 0,25, £_z = 4, X = 0,02.

Uwaga: Pominąć stratę na długości w krótkiej, poszerzonej części przewodu.

5.2.11. O ile procent można zwiększyć przepustowość rurociągu, skracając jego długość o 25%? Założyć, że przed i po skróceniu rurociągu, w przepływającej cieczy panuje jednakowe ciśnienie początkowe. Zagadnienie rozwiązać dla przepływu laminarnego i burzliwego.

5.2.12. (Rys. 1-5.23). Pojedynczy rurociąg AB o długości / łączy dwa zbiorniki. Obliczyć procentowy wzrost objętościowego natężenia przepływu, jeżeli w miejsce

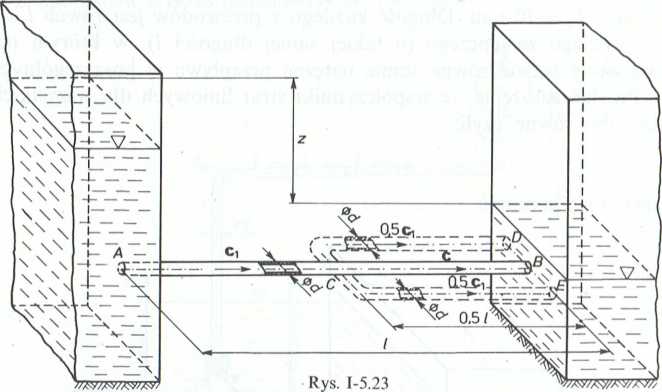
odcinka BC = 0,5 / zostaną zainstalowane dwie równoległe nitki rurociągu CD i CE o takiej samej średnicy d i długości 0,5 /. W obliczeniach uwzględnić tylko straty liniowe oraz przyjąć, że współczynniki strat (dla każdego z przypadków) są równe X.

5.2.13. (Rys. 1-5.24). Dwa zbiorniki połączono układem przewodów rozgałęzionych o średnicach: d_u d₂, d₃, d_A i d₅ oraz długościach: l_t, l₂, Z₃, Z₄ i i₅. Różnica poziomów zwierciadeł cieczy w obu zbiornikach wynosi H. Pomijając straty lokalne (miejscowe)

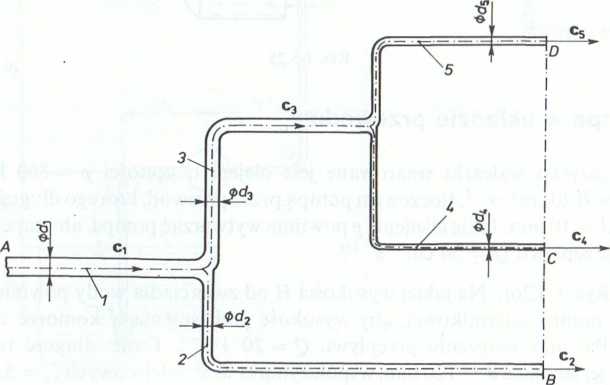
Rys. 1-5.24