P1070052

30 Część I. Przykłady i zadania

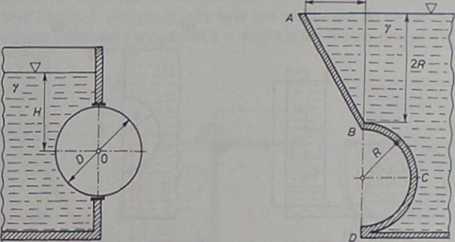
23.19. (Rys. 1-2.45). W pionowej ścianie zbiornika, wypełnionego cieczą o ciężarze właściwym y, znajduje się prostokątny otwór, w który wstawiono wałec o średnicy D i tworzącej poziomej równej L. Walec może obracać się wokół centralnej osj 0, leżącej na głębokości H. Udowodnić, że wypadkowy napór hydrostatyczny nie wywołuje momentu obrotowego walca (paradoks Żukowskiego).

30 Część I. Przykłady i zadania

Rys. 1-2.45

Rys. 1-2.46

23.20. (Rys. 1-2.46). Wyznaczyć wartość oraz kierunek całkowitego naporu hydrostatycznego, jaki wywiera ciecz o ciężarze właściwym y na ścianę ABCD zbiornika. Część AB ściany jest płaska i nachylona, a BCD stanowi połowę pobocznicy walca o promieniu równym R. Szerokość zbiornika, mierzona w kierunku prostopadłym do płaszczyzny rysunku, wynosi b.

Rys. 1-2.47

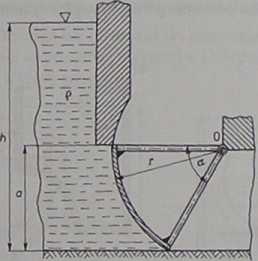
23.21. (Rys. 1-2.47). W sztolni o szerokości b = 5 m, wypełnionej wodą do wysokości h = 4 m, znajduje się obrotowa zapora segmentowa o wymiarach: a = 2 m, kąt a = §. Wyznaczyć moduł, kierunek oraz współrzędne punktu przyłożenia siły naporu działającej na zaporę.

2.4. Pływanie ciał

2.4.1. (Rys. 1-2.48). W naczyniu, którego pole powierzchni dna jest równe A, znajduje się ciecz o gęstości p. Wysokość naczynia wynosi H, a powierzchnia swobodna cieczy jest oddalona o h od dna. Jaką maksymalną objętość V_k może mieć ciało o gęstości p_k < p, aby po jego zanurzeniu ciecz nie wylała się z naczynia?

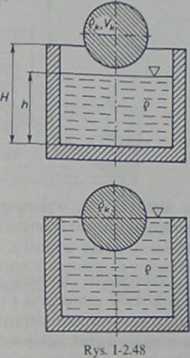
2.4.2. (Rys. 1-2.49). Jednorodna kula o gęstości p, pływa w dwóch nie mieszających się cieczach o gęstości p₂ i p₃. Powierzchnia graniczna cieczy przechodzi przez środek kuli. Określić zależność zachodzącą między tymi trzema gęstościami.

__-i -ptwnetrze

-/TV--

-Ł-

£|S

-P-

Rys. 1-2.50

2.4.3. (Rys. 1-2.50). Nurek kartezjański (np. w postaci probówki) o ciężarze G został zanurzony w wodzie o gęstości p. Na skutek działania siły wyporu, pochodzącej od powietrza o masie m zawartego w probówce, pływa on w wodzie na głębokości z. Zewnętrzne ciśnienie powietrza wynosi p„, a temperatura jest równa T.

a. Jaki warunek muszą spełniać wielkości podane w zadaniu, aby zanurzony nurek był w stanie równowagi?