CCF20120509005

Część I. Przykłady i zadania

kowicie zatopiony. Różnica wysokości poziomów niwelacyjnych zwierciadeł cieczy nosi h, prędkość dopływu — c„, odpływu — c,, a współczynnik objętościowego tężenia przepływu jest równy p.

3. Reakcja strumienia cieczy, oment pędu (kręt)

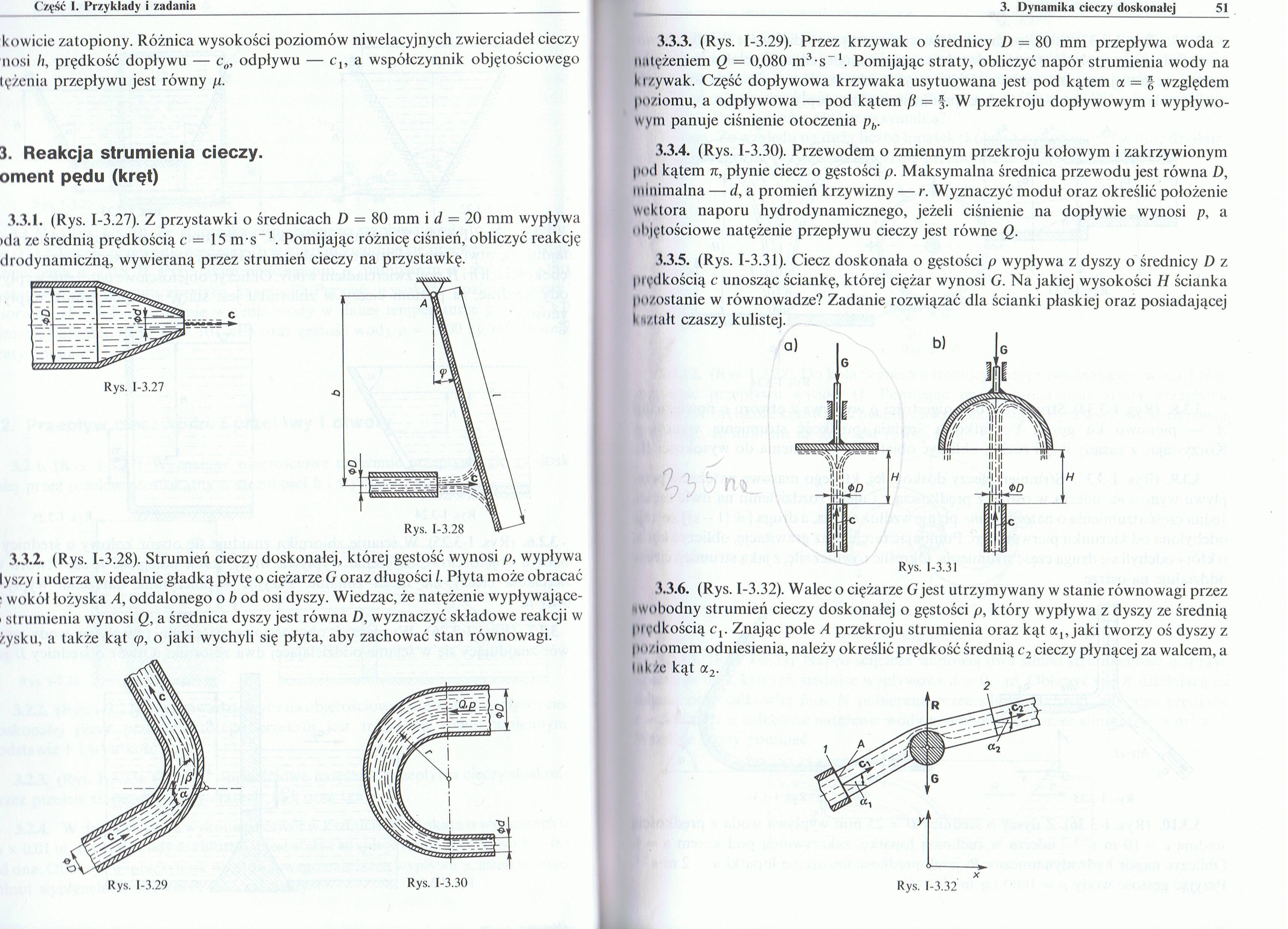
3.3.1. (Rys. 1-3.27). Z przystawki o średnicach D = 80 mm i d = 20 mm wypływa >da ze średnią prędkością c = 15 m-s^-1. Pomijając różnicę ciśnień, obliczyć reakcję drodynamicżną, wywieraną przez strumień cieczy na przystawkę.

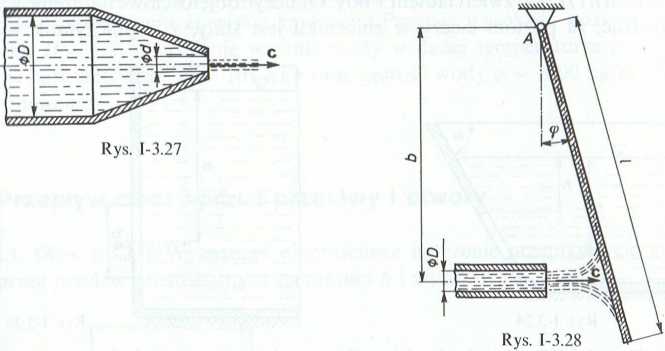
3.3.2. (Rys. 1-3.28). Strumień cieczy doskonałej, której gęstość wynosi p, wypływa lyszy i uderza w idealnie gładką płytę o ciężarze G oraz długości /. Płyta może obracać ■ wokół łożyska A, oddalonego o b od osi dyszy. Wiedząc, że natężenie wypływające-i strumienia wynosi Q, a średnica dyszy jest równa D, wyznaczyć składowe reakcji w żysku, a także kąt cp, o jaki wychyli się płyta, aby zachować stan równowagi.

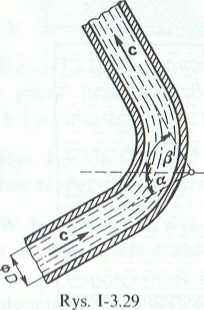
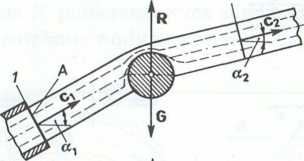
3.3.3.    (Rys. 1-3.29). Przez krzywak o średnicy D = 80 mm przepływa woda z natężeniem Q = 0,080 m³-s^_1. Pomijając straty, obliczyć napór strumienia wody na krzywak. Część dopływowa krzywaka usytuowana jest pod kątem a = | względem poziomu, a odpływowa — pod kątem /i = f. W przekroju dopływowym i wypływowym panuje ciśnienie otoczenia p_h.

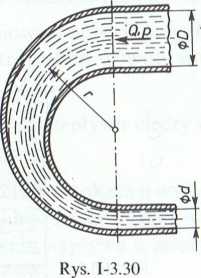
3.3.4.    (Rys. 1-3.30). Przewodem o zmiennym przekroju kołowym i zakrzywionym pod kątem n, płynie ciecz o gęstości p. Maksymalna średnica przewodu jest równa D, minimalna — cl, a promień krzywizny — r. Wyznaczyć moduł oraz określić położenie wektora naporu hydrodynamicznego, jeżeli ciśnienie na dopływie wynosi p, a objętościowe natężenie przepływu cieczy jest równe Q.

3.3.5.    (Rys. 1-3.31). Ciecz doskonała o gęstości p wypływa z dyszy o średnicy D z prędkością c unosząc ściankę, której ciężar wynosi G. Na jakiej wysokości H ścianka pozostanie w równowadze? Zadanie rozwiązać dla ścianki płaskiej oraz posiadającej I t/lalt czaszy kulistej.

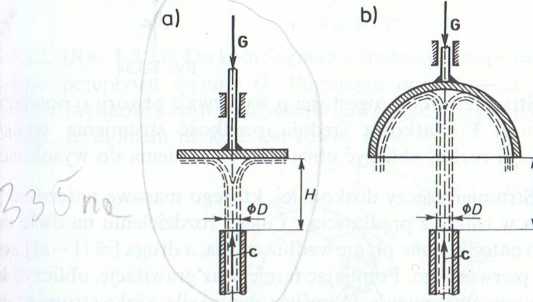
H

Rys. 1-3.31

3.3.6. (Rys. 1-3.32). Walec o ciężarze G jest utrzymywany w stanie równowagi przez •twobodny strumień cieczy doskonałej o gęstości p, który wypływa z dyszy ze średnią prędkością c_l. Znając pole A przekroju strumienia oraz kąt a,, jaki tworzy oś dyszy z I o i/iomem odniesienia, należy określić prędkość średnią c₂ cieczy płynącej za walcem, a luk że kąt a₂.

2

y‘

Rys. 1-3.32

X