CCF20120509020

KO Częsc I. Przykłady i zadania

oraz zakładając, że końce B, C i D przewodów znajdują się na tym samym poziomie, ułożyć równania umożliwiające obliczenie prędkości w poszczególnych odgałęzieniach.

5.2.14. (Rys. 1-5.25). Woda ze zbiornika A jest doprowadzona do zbiornika B trzema przewodami o średnicach wynoszących odpowiednio: d_l = 30 mm, d₂ — 50 mm i d₃ = 70 mm. Długość każdego z przewodów jest równa /. Obliczyć średnicę rurociągu zastępczego (o takiej samej długości /), w którym natężenie przepływu wody będzie równe sumie natężeń przepływu w poszczególnych przewodach. Przyjąć założenie, że współczynniki strat liniowych dla wszystkich rurociągów są sobie równe, czyli:

Aj = A₂ ~ A₂ — A.

Straty miejscowe pominąć.

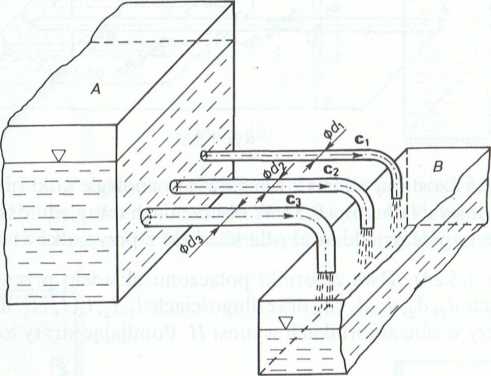
Rys. 1-5.25

5.3. Pompa w układzie przewodów

5.3.1.    Łożysko walcarki smarowane jest olejem o gęstości p = 860 kg-m“³ i lepkości v = 0,20 cm² • s“¹, tłoczonym pompą przez przewód, którego długość / = 6 m, a średnica d = 10 mm. Jakie ciśnienie p powinna wytwarzać pompa, aby zapewnić stałe natężenie przepływu Q = 50 cm³-s^_1?

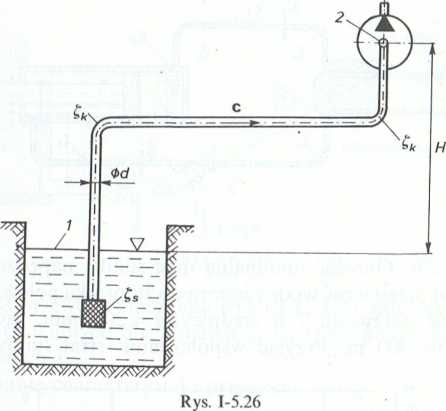
5.3.2.    (Rys. 1-5.26). Na jakiej wysokości H od zwierciadła wody powinna znajdować się oś pompy odśrodkowej, aby wysokość podciśnienia w komorze ssącej p = = 0,05 MPa, przy natężeniu przepływu Q = 20 1-s^-1. Dane: długość rury ssącej / = 12 m, a jej średnica d = 120 mm, współczynniki strat: miejscowych £_s = 5, £_k = 0,25 i liniowych A = 0,03.

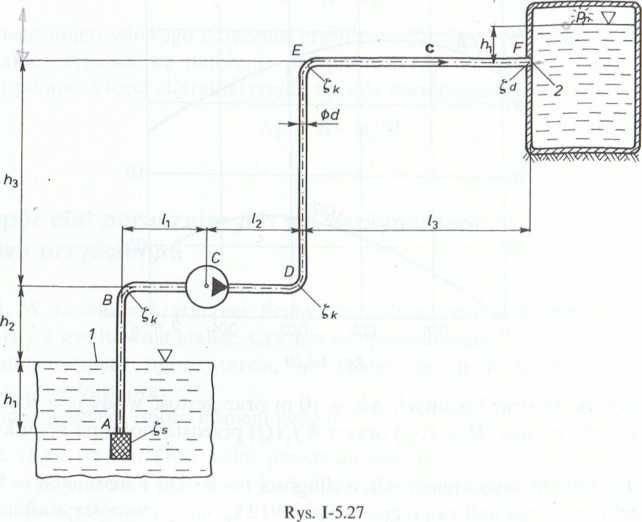
5.3.3. (Rys. 1-5.27). Obliczyć minimalną moc silnika niezbędnego do napi pompy przetłaczającej wodę w ilości Q = 0,01 m³-s^-1, przez przewód o średr d = 60 mm do zbiornika, w którym nadciśnienie wynosi p_n = 0,1 MPa. Da h_t = h₂ = 4 m, h₃ = 12 m, h_A = 2 m, /_t = l₂ = 4 m, Z₃ = 20 m, C_s = 5, £_k = 0,3,    =

współczynnik lepkości kinematycznej wody v = 0,01 cm²-s^-1, sprawność por p = 0,72. Sporządzić wykres piezometryczny i energetyczny.

6 — Mechanika nłvnów