CCF20120509014

<>N Część 1. Przykłady i zadania

Wyznaczyć:

a)    pole wektorowe przyspieszeń,

b)    przyspieszenie w punkcie K(2, 1),

c)    równanie linii prądu przechodzącej przez punkt K(2, 1).

4.5.3.    Funkcja prądu

i/f = 4 x —2 y

opisuje płaski przepływ płynu doskonałego.

a.    Sprawdzić, czy jest spełnione równanie ciągłości przepływu.

b.    Określić pole prędkości przepływu v.

c.    Wyznaczyć potencjał prędkości ę.

4.5.4.    Wyznaczyć objętościowe, jednostkowe natężenie przepływu płynu doskonałego przez odcinek łączący punkty A (0,0) i B(2,2). Przepływ płynu określa potencjał prędkości:

ę(x, y) = ax³ — 3axy²,

gdzie a = const ^ 0.

4.5.5.    Płaski, nieustalony przepływ płynu doskonałego określa wektor prędkości:

v = ai + (b + ct)j,

gdzie a = const ^ 0, b = const ^ 0 i c = const ^ 0. Wyznaczyć:

a)    równanie rodziny linii prądu,

b)    równanie rodziny torów poruszania się elementów płynu.

4.5.6.    Dany jest potencjał zespolony:

w(z) = az,

gdzie a jest liczbą rzeczywistą. Wyznaczyć oraz przedstawić graficznie rodzinę linii ekwipotencjalnych i linii prądu, a także zaznaczyć na nich kierunek przepływu.

4.5.7.    Przepływ płynu doskonałego określa potencjał zespolony:

w(z) = £az²,

przy czym a jest liczbą rzeczywistą.

a.    Wyznaczyć i przedstawić graficznie rodzinę linii prądu oraz rodzinę linii ekwipotencjalnych.

b.    Określić składowe oraz moduł wektora prędkości.

4.5.8.    Potencjał zespolony:

3

w(z) = faz 2",

w którym a jest liczbą rzeczywistą, określa płaski przepływ płynu doskonałego. Korzystając z układu współrzędnych biegunowych, wyznaczyć oraz przedstawić graficznie funkcję prądu .9) oraz określić składowe i moduł wektora prędkości.

(p(x, y) = x\n^/x² + y² — yaretg

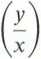
4.5.9. Funkcja

jest potencjałem prędkości płaskiego, ustalonego ruchu płynu doskonałego. Określić funkcję prądu i//(x, y) oraz potencjał zespolony w(z).

4.5.10. Płaskie przepływy płynu doskonałego opisano składowymi wektora prędkości:

a) v_x = 4 ay, v_v = 0,

^b) ”^x x²+y²’

^vy =

y

x² + y²'

Zbadać, czy dane przepływy są wirowe. Jeśli tak, wyznaczyć natężenie wiru, czyli strumień wirowości.

4.5.11.    Obliczyć cyrkulację prędkości po konturze okręgu o średnicy d — wiedząc, że wektor prędkości, określający przepływ płynu doskonałego:

v = 4yi — 4xj.

4.5.12.    Przepływ płynu doskonałego został wytworzony przez źródło wirowe, które jest superpozycją źródła o natężeniu Q i wiru o cyrkulacji F, znajdujących się w początku układu osi współrzędnych. Wiedząc, że potencjał zespolony źródła wynosi

{Q/2%)\nz, a wiru (F/2Jtijlnz, wyznaczyć oraz przedstawić graficznie rodzinę linii prądu.

4.5.13.    Korzystając z rozwiązania przykładu 4.4.5., wyznaczyć rozkład ciśnienia na obwodzie walca o promieniu r, który jest opływany płynem o gęstości p, poruszającym się ze stałą prędkością v_OT. Ciśnienie płynu w obszarze niezakłóconym wynosi p„.