CCF20120509002

V,/,pt I. /•j Kłulij i /.auuiiia 3. Dynamika cieczy doskonalej 4t>

V,/,pt I. /•j Kłulij i /.auuiiia 3. Dynamika cieczy doskonalej 4t>

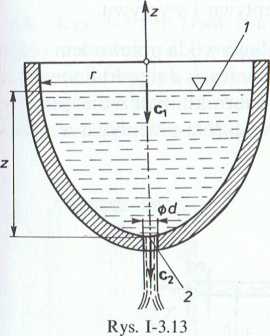
3.1.11. (Rys. 1-3.10). Ciecz doskonała o gęstości p przepływa przewodem rurowym, który łączy dwa zbiorniki jak na rysunku. Różnica poziomów cieczy w zbiornikach wynosi H, a pozostałe wymiary są równe h_{ i h₂. Należy sporządzić wykres Iłcrnoulliego oraz wyprowadzić warunek, jaki musi być spełniony, aby w najwyżej położonym przekroju przewodu nie wystąpiło zjawisko kawitacji. Przyjąć ciśnienie wrzenia cieczy równe p_w, a ciśnienie barometryczne p_h.

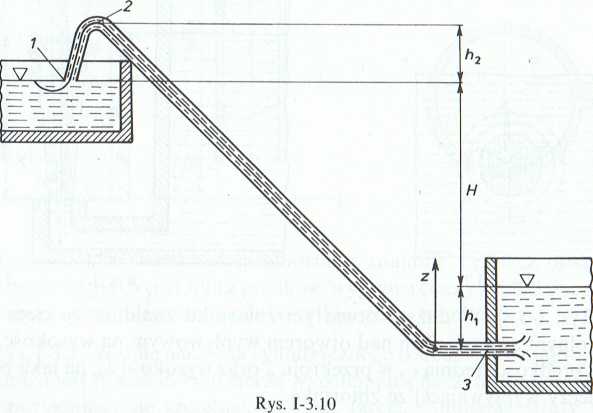
3.1.12. (Rys. 1-3.11). Jaka jest prędkość przepływu płynu o gęstości p, w którym zanurzono rurkę Prandtla, jeżeli w podłączonym do niej manometrze różnica poziomów cieczy wynosi hl Przyjąć gęstość cieczy manometrycznej równą p_m.

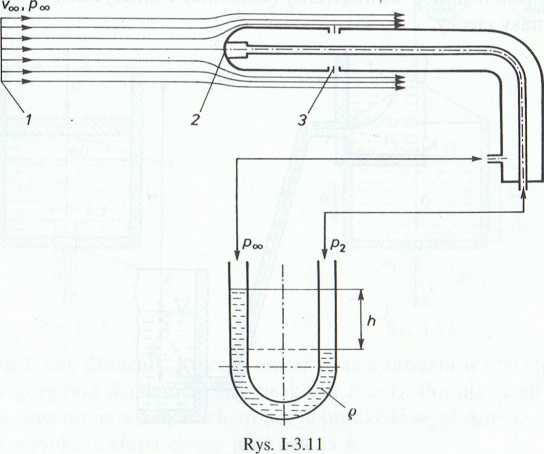
3.1.13. (Rys. 1-3.12). Do budynku doprowadzono wodę z dużego zamkniętego zbiornika, w którym panuje ciśnienie absolutne p_;, a odległość zwierciadła wody od lundamentu wynosi h = const. Obliczyć prędkość wypływającej wody na poszczególnych kondygnacjach, jeżeli dana jest odległość a. Określić również prędkość c, w podziemnej części przewodu doprowadzającego o przekroju A_x, wiedząc, że wszystkie przekroje przewodów wypływowych wynoszą A. Gęstość wody przyjąć równą p, a

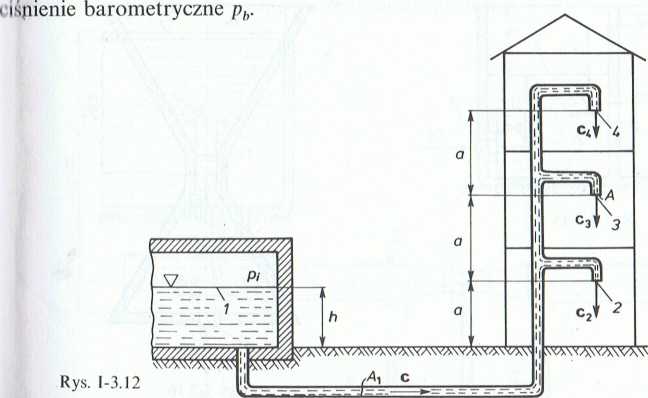
3.1.14. (Rys. 1-3.13). W czasach starożytnych używano szklanych zegarów wodnych, których kształt był tak dobrany, że lustro wody opadało ze stałą prędkością c_x. Wyznaczyć funkcję opisującą kształt czaszy zegara z = /(r), jeżeli średnica otworu wypływowego wynosi d.

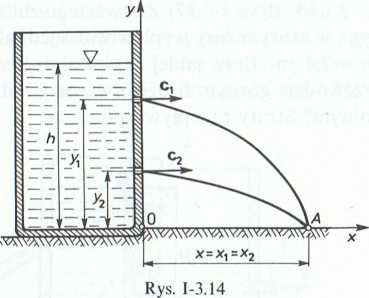
3.1.15. (Rys. 1-3.14). W pionowej ścianie zbiornika wykonano dwa małe otwory, z k tórych górny położony jest w odległości y_x, a dolny w odległości y₂ od dna. Strumienie Nwobodne, wypływające przez otwory, uderzają w płaszczyznę poziomą w tym samym punkcie A. Znaleźć zależność pomiędzy y_x i y₂, jeżeli wysokość cieczy w naczyniu wynosi h.