6830720104

Szacowanie rezystancji uzwojenia strony pierwotnej i wtórnej :

Moc znamionowa transformatora :    Sn = 2,1 kW.

Prąd znamionowy strony pierwotnej : Iin = 5,5 A.

Prąd znamionowy strony wtórnej :    I2N = 17 A.

Zakładamy sprawność transformatora T] = 0,95 .

Wówczas straty mocy stanowią : AP = Po, + PFe = 0,05*Sn .

Zakładamy stosunek mocy : Po/PFe = 2,5 , więc AP = 3,5* PF_e = 105 W . Otrzymano : PFe= 30 W , Pcu= 75 W .

Na jedną fazę dowolnej strony tr - ra przypadają straty równe 1/6 strat całkowitych w uzwojeniach , więc :

Ri = Pcu/6Iin² - rezystancja strony górnego napięcia R2 = Pcu/6I2n² - rezystancja strony dolnego napięcia Oszacowano : Ri = 0,413 O, R2 = 0,043 .

Wyznaczanie sprawności transformatora.

Sprawność transformatora określa się jako stosunek mocy czynnej oddawanej P2 do mocy czynnej pobieranej Pi.

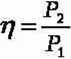
Na podstawie wyników w stanie zwarcia można określić straty w uzwojeniach Pcun przy prądzie znamionowym Iin jako:

PCuN ~

Korzystając z wyników pomiaru stanu jałowego można określić wartość strat w rdzeniu Pfcn przy zasilaniu transformatora napięciem znamionowym:

IN

U.

FeN

R

Fe

Zakładając niezmienny współczynnik obciążenia np. cos(|> = 0.8, oraz znając wartość mocy znamionowej transformatora Sn = 2.1kW, zmieniając wartość współczynnika względnego obciążenia I_rei od 0.2 do 1.2 możemy obliczyć wartość sprawności transformatora

Sff/rei COSę?+ I_r^P_Cljf + Pp_eN

Irel	Irei^2	O S(j)2	Irel PcuN	Tl
-	-	[W1	[W]	-
0.2	0.04	336	3	0.910
0.4	0.16	672	12	0.941
0.6	0.36	1008	27	0.946
0.8	0.64	1344	48	0.945
1.0	1.0	1680	75	0.941
1.2	1.44	2016	108	0.935