7404701565

Rozkłady naprężeń w gruncie wywołane siła skupioną Teoria Bussinesq'a: Obecnie do wyznacz naprężeń w gruncie stosuje się najczęściej rozwiązania oparte na teorii sprężystości Równania teorii sprężystości dla zagadnień przestrzennych mają bardzo skomplikowaną postać i dlatego stosuje się je w praktyce tylko jedynie do pewnych wybranych problemów.Najczęściej znajdują zastosowanie rozwiązania uzyskane dla elementarnych przypadków. Jednym z takich przypadków jest rozwiązanie Boussinesq'a dla rozkładu naprężeń w półprzestrzeni sprężystej obciążeń na brzegu siłą

skupioną.

Hipoteza Boussinesaa jest oparta na następujących założeniach:

ljpodłoże gr stanowi półprzestrzeń ogranicz od góry płaszczyznąa nieograniczoną w pozostałych kierunkach

2}gr jest materiałemizotropowym,a wiec mającym jednak właściwości sprężyste we wszystkich kier oraz materiałem nieważkim (y=0)/3)przyjmuje się w praktyce zależność liniową między naprężeniem a odkształceniem a wiec obowiązuje prawo Hooke'a/

4) obowiązujezasada superpozycji a zatem sumują się napręż od działania różnych obciążeń

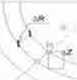
5) sposób przyłożenia obciąż zgodnie z zasada Saint-Venanta wpływa na rozkład naprężeń tylko w bliskim sąsiedztwie miejsca przylożonegoobciażenia./Oznaczmy naprężenia promieniowe dla dowolnego punktu M przez <r_R a dla punktu K przez a_R0< E-współczynnik sprężystości gruntu a AZ pionowe przesunięcie całej półkuli pionowo w dół, wtedy:AZ=const./ AZ=AR/cosP/AR=AZcosfl// W myśl prawa Hooke'a: AR=6R(indeks)d/E; AZ= 6R(indeks)d/Ecos0; ARo= 6RO{indeks)d/E

* <?m

Izo bary pionowych naprężeń normalnych

Rozkład naprężeńcrZ w gruncie na różnych głębokościach od obciążenia siłą skupioną