7488178711

prostopadły do promienia wodzącego r. a nie do aktualnego promienia krzywizny (rysunek). Przy opisie ruchu po okręgu zachodzą pomiędzy weroorami proste relacje:

t - s, oraz    r - - n.

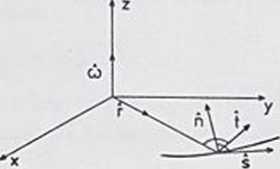
Gdy w jest wereorem osiowym (wersorem wektora obrotu), to *>-*><-> oraz    dp - d?xo.

Przemieszczenie infimtezyma1ne w ruchu po okręgu przedstawimy za pomocą poznanych wersorów;

dr - dss ■ r dł> 3 ■ r ds> t ■ r dę> oxr.

dr - cip (wxr) - d?>xr.

Warto zauważyć. że otrzymana relacja jest słuszna dla dowolnego wektora A

dA - d»>xA - dę> (wxA) .

W dalszej części będziemy korzystać z wielkości dr. którą otrzymujemy korzystając z powyższego wzoru

dr - dp (wxr) - d*> t.

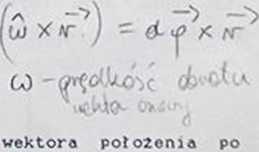
d, * ■> d

3.2. Prędkość i Przyśpieszenie Pfftflkftiłri* liniowa J03t pochodna

czasie