1098873055

3. Skonstruuj odpowiednią bazę Newtona i rozwiąż, metodą różnic dzielonych, zadanie interpolacyjne Hermite’a dla danych w tabelce:

X	-1	1	2
f(x)	5	5	2
f'(x)	-4		-16
f"(x)	-4
f"'(x)	-24

4. Funkcję f(x) = sinx w przedziale [0,tt] przybliżamy

a)    wielomianem interpolacyjnym Lagrange’a stopnia 2n — 1 opartym na węzłach Czebyszewa w tym przedziale,

b)    wielomianem interpolacyjnym Hermite’a stopnia 2n — 1 opartym na dwóch węzłach: 0 i 7t, z których każdy ma krotność n,

c)    interpolacyjną funkcją sklejaną stopnia 1, której węzły dzielą przedział [0,7t] na 2n — 1 podprzedziałów o jednakowej długości 7t/(2n — 1); węzły te są jednocześnie węzłami interpolacyjnymi.

Podaj górne oszacowanie błędu aproksymacji jednostajnej w każdym z tych przypadków, w zależności od n. Możesz w oszacowaniach użyć równości przybliżonej n¹ « 10.

5. Rozważamy iloczyn skalarny

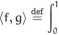
f(x)g(x)xdx.

a)    Znajdź pierwsze trzy wielomiany z rodziny wielomianów ortogonalnych w sensie tego iloczynu skalarnego.

b)    Korzystając z wyniku punktu a), skonstruuj kwadraturę Gaussa rzędu 2 przybliżającą całkę

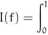
f(x)xdx

1

znajdź oszacowanie błędu tej kwadratury dla funkcji f klasy C²[0,1].