str169 (3)

>WAN1A § 5. WYZNACZANIE ROZWIĄZANIA RÓWNANIA RÓŻNICZKOWEGO RZĘDU n 169

>WAN1A § 5. WYZNACZANIE ROZWIĄZANIA RÓWNANIA RÓŻNICZKOWEGO RZĘDU n 169

i obu stron równania, jako

4L(1).

igę warunek (2), mamy )+4L(l).

"s*

iztalceniach

Z tablicy przekształceń Laplace’a odczytujemy

1

(4')    L(l) = — (por. wiersz 1).

Zgodnie z wzorem (1.8) mamy

(5)    L(y") = S²L(y)-Sy(+0)-y'(+0),

(6)    L(/) = SLOO-y(+0).

Podstawiając związki (5), (6) i (4') do wzoru (4), mamy po przekształceniacli (7)    (S²—S—2)L(y) = Sy(+0)-y'(+0)-y(+0)+j.

Uwzględniając w (7) warunki

y(+0) = y(0) = l,    y'(+0) = /(0) = 0,

mamy po przekształceniach

(8)

L(y) =

S²-S +1 S(S² — S—2)'

1_

+3‘

enie Laplace’a, marny

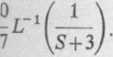
i >

Rozkładamy prawą stronę na ułamki proste:

(9)

, _% 111

L(y) ------1---

2 S 2

1 1 S—2 ⁺ S + l '

Stosując po obu stronach (9) odwrotne przekształcenie Laplace’a, mamy na mocy wzoru (3.2)

(.o    ł^Ł’^,(j)⁺*^ir,G^)^+ir,Gił)-

Z tablicy odczytujemy (por. wiersz 1 i wiersz 2):

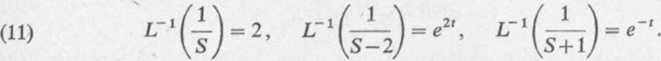
Uwzględniając równości (11) we Wzorze (10), otrzymujemy szukane rozwiązanie

y— —i + -Je^2, + e

Zadanie 5.3. Znaleźć rozwiązanie równania

(1)

spełniające warunki początkowe

/' + A²y = 0,