81757 str173 (3)

S0WANIA § 5. WYZNACZANIE ROZWIĄZANIA RÓWNANIA RÓŻNICZKOWEGO RZĘDU 173

iie przekształcenie Laplace’a.

= 0.

SV^3,(+0)-

-0)—Sy^w(+0)-y^(7,(+0),

s²y³⁾(+o)-

-S/^4>(+0)-v^<5,(+0),

>■

niając warunki początkowe (2)

IS² + 5,

•3S² + 5 )(S²+1)³‘

emy

przekształcenia Laplace’a

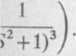
»r. wiersz 2).

powiednich wzorach z tablicy

4/ sin f] * sin t = f²) sini-4* cos t].

Ostatecznie

(10)    ¹ ^^l+]y) = (ł -ł<²)^sin < -ł< cos t.

Podstawiając wzory (9) i (10) do równania (8), otrzymujemy szukane rozwiązanie

y = e'—e~'— 4(3 — t²)sint + ftcosf.

Zadanie 5.6. Rozwiązać równanie

(1)    y"(t)-y\t)-2y(t) = e' przy warunkach początkowych

(2)    y(0) = 1, y'(0) = 0.

Rozwiązanie. Stosujemy do równania (1) obustronnie przekształcenie Laplace’a. Otrzymujemy w'tedy

L[y"(0-/(0-2y(0] = L(e').

Korzystając ze wzoru (1.6) mamy

(3)    L[y"]-L(y')-2L(y) = L(e').

Z tablicy przekształceń Laplace’a, § 8, odczytujemy

(3')

L(e') = —-S-l

(por. wiersz 2).

Na mocy wzoru (1.8) wyliczamy dalej

(4)    L(y") = S²L(y)-Sy( + 0)-y'( + 0),

(5)    L(y') = SL(y)-y( + 0).

Podstawiając wzory (4), (5) i (3') do równania (3) oraz wykorzystując warunki początkowe (2) otrzymujemy po przekształceniach i uporządkowaniu

(S² —S —2)L(y) = S—1 +

1

S-l’

a stąd

(7)

L(y) =

-S + 2

(S — S —2)(S — 1)

Rozkładając prawą stronę równania (7) na ułamki proste, mamy

1

1 1 2 L(y)=    — +

5    1

+—.

2 S-l 3 S—2    6 S+l

(8)