str175 (3)

OWANIA 9 5. WYZNACZANIE ROZWIĄZANIA RÓWNANIA RÓŻNICZKOWEGO RZĘDU n 175

rotne względem przekształce-

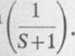
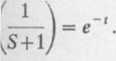
kane rozwiązanie

nie przekształcenie Laplace’a.

')•

ykorzystując warunki począt-aniu

amy

1

(S+2)²+9] ‘

Stosując do równania (9) obustronnie przekształcenie odwrotne Laplace’a i wykorzystując jego liniowość, mamy

(10)    y = r^L    ((s₊2)²+9~)^_tL ((S+2)²+"ó)’

Z tablicy przekształceń odczytujemy (wiersz 2, 6, 7):

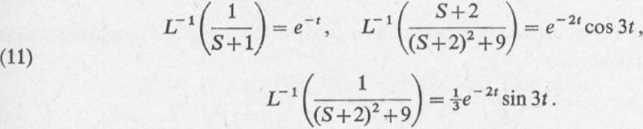
Podstawiając związki (11) do wzoru (10), otrzymujemy

y =    ‘—\e ^2,cos3t —fe ^2,sin31

lub

e~'—e~ ²'(cos 3t + 2 sin 3t)

Zadanie 5.8. Znaleźć rozwiązanie równania

(1)    y”—2y'+y = 1 przy warunkach początkowych

(2)    y( 0) = 0, y'(0) = 1 •

Rozwiązanie. Stosujemy do równania (1) obustronnie przekształcenie Laplace’a. Wykorzystując następnie wzór (1.6) mamy

(3)    L(y")—2L(y') + L(y) = L(l).

Na mocy wzoru (1.8) mamy

(4)    L(y") = S²L(y)-SH+0)-yX+0).

(5)    L(y') = SL(y)-y( + 0).

Oprócz tego z tablicy przekształceń odczytujemy

(6)    Ml)-y.

Podstawiając wzory (4), (5) i (6) do równania (3) oraz wykorzystując warunki początkowe (2), otrzymujemy po przekształceniach i uporządkowaniu

(7)    (S²-2S+1)LOO = 1 + 1,