88472 str181 (3)

WANIA 8 5. WYZNACZANIE ROZWIĄZANIA RÓWNANIA RÓŻNICZKOWEGO RZĘDU 181

)o przekształceniach

L(z), otrzymujemy )²~1

-1)²+1]'

ie przekształcenie odwrotne

((S-1)[(S-1)² +

—) = e' cos /.

-1/

korzystając z (10), że

gdzie

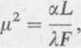
L — obwód przekroju poprzecznego pręta, F—pole powierzchni tegoż przekroju, a — współczynnik przejmowania ciepła, X — przewodność właściwa ciepła.

Transformujemy obecnie równanie (1), przyjmując następujące oznaczenie T(S) —

S²T(S)-St(0)~l\0)-n²T(S) = 0,

stąd po uwzględnieniu warunku t'(0) = 0 mamy

(3)

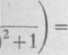
inidr = — e'cos t + e'.

:os t).

długości 2a dopływa stały mperatury t(x) wzdłuż pręta ym, jeżeli jego powierzchnia

przyrostem temperatury pręta inkcja t(x) spełnia równanie

Funkcja T(S) ma dwa bieguny jednokrotne

Sj = — fi, S₂= fi.

Wyznaczamy obecnie oryginał /(jc) funkcji (3) stosując wzór (3.5)

t(x)= V res [T(S)/"] = T(0) V lim    =

/ J s = J)c    / J S—Sk ^ i¹

fc=l    k=1

= f(0)

r e^s,x ł^lX 1 U-S₂ s₂—s,J

t (0) cosh fix.

Dla wyznaczenia /(O) stosujemy drugi z warunków (2) i otrzymujemy końcową postać funkcji /(a-) opisującej pole temperatury w rozważanym pręcie

q cosh fix

<(*) =

X sinh fia

Zadanie 5.14. Funkcja x(l) opisująca drganie tłumione punktu materialnego (rys. 3.6) spełnia równanie różniczkowe

(1)

M

d²x dx

+H — + kx(t) = f(t),

dt² ' ^r' dt

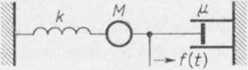
Rys. 3.6

x

gdzie M — masa, n — współczynnik tłumienia, k — stosunek siły zwracających drgań własnych do wychylenia, /(/) — siła wymuszająca drgania (rys. 3.6).Wyznaczyć funkcję *(/), jeżeli w chwili t = 0 rozważany punkt materialny znajduje się w spoczynku i przyjmując