34289 str183 (3)

WANIA 9 5. WYZNACZANIE ROZWIĄZANIA RÓWNANIA RÓŻNICZKOWEGO RZĘDU n 183

:dnich jednostkach [/] = N, biera postać

t=o

i,(t)

ającym następujące warunki

i oznaczenie x(S) = a[x(f)] 10

^lS,-ś^4-

(jestbiegunem dwukrotnym, wzór (3.5)

(1)

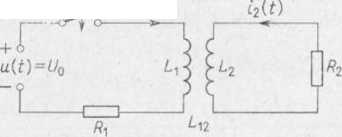
Rys. 3.7

Rozwiązanie. Natężenia prądów i\(t) oraz i₂(t) spełniają następujący układ równań różniczkowych:

di,    di₂

Li —+ L_ł2—+Rii'i =*= u(f),

di,    di₂

^Ll2~dF^+L2~dt^{+R2h = 0}

oraz następujące warunki początkowe:

(2)    *i(0) = 0,    «₂(r) = 0.

Transformujemy równania układu (1), przyjmując przy tym następujące oznaczenia: /((S) = L[ii(0] , I₂(S) = L[/₂(0] ,

SLJW-LMOHSLMS) -L _i2i₂(0)+ R,/i(S) = j U₀, SL₁₂/₁(S)-L₁₂i₁(0) + SL₂/₂(S)-L₂i₂(0)+R₂/₂(S) = 0, skąd po uwzględnieniu warunków (2) mamy

(3)

(R, +SL₁)/,(S) + SL₁₂/₂(S) = | (/<>,

df^J

i₃ds[_S² + 4j’

odpowiednich przekształceń n2r].

zężone ze sobą magnetycznie ;l ze źródła o napięciu u(t):

«unku 3.7. Wyznaczyć prze-żaden prąd nie płynął w roz-

SL₁₂/!(S) + (R₂ + SL₂) /₂(S) = 0.

Rozwiązaniami układu równań (3) są transformaty I_t(S) oraz I₂(S) o następującej

postaci:

(4)

(5)

/,(S) =

/₂(S) fc.

U ₀R₂ + SL₂

S[S²(L_iL₂-L?₂) + S(R₁L₂ + R₂L,) + R₁R₂]’

u₀l₁₂

S²(L₁L₂-L²2) + S(R₁L₂ + R₂L,) + R,R₂'

Funkcja 7,(5) ma trzy bieguny jednokrotne S₀ = 0,

(6)

₀    ^— RiL₂ — R₂Lj — n/(RiL₂ — R₂L,) +4R,R₂L₁₂

2(LjL₂ —L_l2)

— R_lL₂ — R₂L_t + n/(RiL₂-R₂L₁)²+4R,R₂L?₃ 2(LjL₂ —L²2)