2500335429

Przechodzimy do testowania stabilności parametrów w obu podpróbach. Hipoteza zerowa brzmi: wszystkie szacowane parametry (również stała) są takie same w obu podpróbach. Wprowadzamy następujące oznaczenia: m - liczba wyodrębnionych podpróbek,

K - ilość szacowanych parametrów (ta sama wartość dla wszystkich modeli), n - liczebność próbki wyjściowej.

•    Odczytujemy wartość krytyczną F*(K(m - 1), N - mK)

•    Liczymy wartość statystyki testowej:

F =

(e e-e[e_x-e{e₂ )/[K (/n—1)] (e_t'e₁ +e₂e₁)l(N-mK)

Sprawdzić, czy parametry modelu są stabilne.

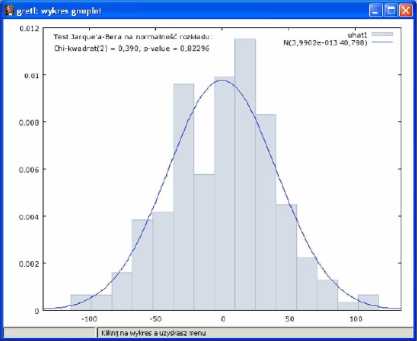
c) Czy reszty mają rozkład normalny ?