2500336021

Zadanie 2.13

Blokiem wymiaru p x q macierzy A = [o,j] nazywamy jej podmacierz utworzoną przez elementy ay leżące na przecięciu ustalonych p wierszy i q kolumn. Na przykład macierz kwadratowa A stopnia n może być podzielona w następujący sposób na cztery bloki

A= \ ^{An A}.¹² 1,

[ ^21 ^22 J

gdzie bloki Au i A22 są macierzami kwadratowymi stopnia k i n — k, odpowiednio. Macierze w postaci blokowej nazywa się też macierzami blokowymi. Działania na macierzach blokowych wykonuje się zgodnie z tymi samymi zasadami, co na macierzach o elementach liczbowych.

Niech macierz kwadratowa B stopnia n będzie podzielona na bloki tak jak powyżej macierz A. Łatwo można pokazać, że iloczyn AB można zapisać w następującej postaci blokowej:

_ r M\B\\ + A12B21, ^n#i2 + A12B22 1

y A2\B\\ + A22B21, A21B12-\-A22B22 J

W szczególności A² można zapisać tak:

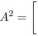
^11-^11 + A12A21, A_nA_u + A12A22 A21 Au + A22A21 , ^21^12 + ^22-^22

(a)    Niech blok A21 będzie zerowy, a bloki przekątniowe A\\ i A22 niech będą nieoso-bliwe. Wykazać (korzystając z definicji macierzy odwrotnej i mnożenia macierzy w postaci blokowej), że wówczas

a-i _ [ ^n¹ -AuAi₂A₂2 1

L 0    ^A22 J*

' 1	2	0	0 '		’ 1	2	0	0 '
2	1	0	0	, B =	2	1	2	0
0	0	1	2		0	2	1	2
0	0	2	1		0	0	2	1

Macierz A (i B) podzielić na cztery bloki stopnia 2. Zastosować powyższe wzory do obliczenia A², AB i A^-1.

(b)    Niech

Uwaga. Postać blokowa macierzy nie jest w programie wykładu.

Zadanie 2.14

(Eliminacja Gaussa-Jordana) W trakcie eliminacji Gaussa, zastosowanej do układu równań liniowych z nieosobliwą macierzą, układ jest przekształcany do układu równoważnego z macierzą trójkątną górną (z ewentualnym przestawianiem równań, czyli wierszy macierzy układu i prawej strony). Proces ten można kontynuować przekształcając układ do układu z macierzą przekątniową (za pomocą elementarnych przekształceń "zerując” elementy macierzy układu powyżej głównej przekątnej), który bardzo łatwo można rozwiązać. Metoda ta nazywa się eliminacją Gauss a-Jordana. Rozwiązać za pomocą eliminacji Gaussa-Jordana, któryś z układów równań liniowych podany w poprzednich zadaniach.

16