7090996909

W. Guzicki: Zadania z kombinatoryki 13

Te obszary także nazywamy składowymi. A więc okręgi należy narysować tak, by wszystkie składowe były niepuste. Następnie w każdy obszar wpisujemy liczbę oznaczającą, ile elementów ma zbiór odpowiadający temu obszarowi. Obszary te zapełniamy w kolejności numerów wpisanych w nie na ostatnim rysunku; zaczynamy więc od obszaru oznaczonego liczbą I. W ten obszar, odpowiadający części wspólnej BnSflW, wpisujemy liczbę 3, bo 3 uczniów gra we wszystkie trzy gry. Następnie w obszar z numerem II wpisujemy liczbę 4. Wiemy bowiem, że 7 uczniów gra w brydża i w szachy, a 3 z nich już uwzględniliśmy w obszarze I (inaczej mówiąc: 3 z nich gra ponadto w warcaby, a więc zostaje 4, którzy grają tylko w brydża i szachy). Mamy zatem rysunek:

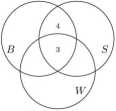
W podobny sposób wpisujemy liczby 2 i 1 w obszary o numerach III i IV:

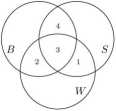
Następnie w obszar o numerze V wpisujemy liczbę 7. Mianowicie w brydża gra 16 uczniów, a 9 z nich zostało już uwzględnionych (3 w obszarze I, 4 w obszarze II i 2 w obszarze III). Otrzymujemy rysunek:

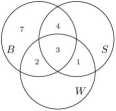
W podobny sposób wpisujemy liczby 5 i 4 w obszary VI i VII:

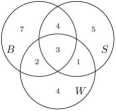
Warszawa, 19-20 października 2013 r.