7090996910

14 W. Guzicki: Zadania z kombinatoryki

14 W. Guzicki: Zadania z kombinatoryki

obszar

W 7 obszarów wpisaliśmy liczby o sumie równej 26. Ponieważ w klasie jest 30 uczniów, więc o numerze VIII wpisujemy liczbę 4 i w ten sposób nasz rysunek jest kompletny:

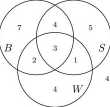
Liczba 4 w obszarze ósmym daje odpowiedź w zadaniu 17, mianowicie 4 uczniów nie gra w żadną z tych trzech gier.

W podobny sposób rozwiązujemy zadanie 18. Znów wpisujemy liczby w obszary w kolejności numerów. Jest jednak pewna różnica: tak jak w zadaniu 16, nie wiemy, ilu uczniów gra we wszystkie gry. Jest to bowiem niewiadoma, którą musimy znaleźć. W obszar o numerze I wpisujemy zatem niewiadomą x. W obszary II, III i IV wpisujemy teraz odpowiednio 6 — x, 7 — xi5 — x. W obszar V musimy wpisać teraz 17 - (6 - x) — (7 — x) — x = x + 4.

— 1. Wreszcie

obszar VIII

W podobny sposób w obszar VI wpiszemy x + 2 i w obszar VII wpiszemy wpisujemy 3, bo 3 uczniów nie gra w żadną grę. Mamy zatem rysunek:

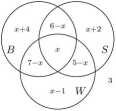
Ponieważ w klasie jest 30 uczniów, więc po dodaniu wszystkich liczb wpisanych w 8 obszarów otrzymujemy równanie

x + (6 - x) + (7 - x) + (5 - x) + (x + 4) + (x + 2) + (x - 1) + 3 = 30, którego rozwiązaniem jest x = 4. Zatem we wszystkie trzy gry jednocześnie gra 4 uczniów.

Uważam, że rozwiązanie graficzne korzystające z diagramów Venna jest dla uczniów bardziej naturalne Zauważmy, że powyżej nie podałem dowodów obu wzorów włączeń i wyłączeń. Nie jest to przypadek Istnieją dowody czysto kombinatoryczne, jednak moje doświadczenie pokazuje, że większość uczniów ma trudności ze zrozumieniem ich. Można też pokazać dowody wykorzystujące kilka prostych równość z rachunku zbiorów. Powstaje jednak wtedy problem, w jaki sposób możemy w szkole dowodzić tożsamość rachunku zbiorów. Sądzę, że najprostszą metodą jest ilustrowanie takich tożsamości na diagramach Venna Popatrzmy na przykładową tożsamość:

{A U B) \ C = (A \ C) U (B \ C).

Zacieniujemy na diagramach Venna zbiory występujące po obu stronach równości. Zajmiemy się najpierw lewą stroną. Najpierw zacieniujemy zbiór AU B:

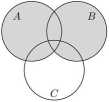
Warszawa, 19-20 października 2013 r.