7090996908

12 W. Guzicki: Zadania z kombinatoryki

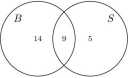
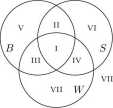
Obszar o numerze III, zawarty wewnątrz lewego okręgu i na zewnątrz prawego, oznacza te elementy, które należą do zbioru B i nie należą do zbioru S. W zadaniu 15 oznacza on tych uczniów, którzy grają w brydża i nie grają w szachy; jest 14 takich uczniów. Podobnie w obszarze IV mamy 5 uczniów, którzy grają w szachy i nie grają w brydża. Te liczby wpisujemy w obszary III i IV:

W trzy obszary wpisaliśmy liczby o sumie 28. Zatem w czwartym obszarze ma być liczba 2:

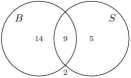
To znaczy, że dwóch uczniów nie gra w żadną z tych gier.

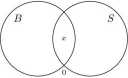
W zadaniu 16 zaczynamy od wpisania liczby 0 w obszar o numerze I i wpisania x w obszar o numerze II.

Teraz w obszar o numerze III wpisujemy 19 — x, a w obszar o numerze IV wpisujemy 14 — x:

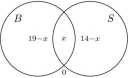
Teraz mamy równanie

(19 - x) + (14 — x) + x + 0 = 30,

skąd łatwo dostajemy x = 3. Zatem trzech uczniów gra w obie gry.

W zadaniu 17 rozważamy trzy zbiory: zbiór B uczniów grających w brydża, zbiór 5 uczniów grających w szachy i zbiór W uczniów grających w warcaby. Dla zilustrowania tych trzech zbiorów rysujemy na płaszczyźnie trzy okręgi, dbając jedynie o to, by były w tzw. położeniu ogólnym, tzn. by dzieliły płaszczyznę na 8 obszarów (ponumerowanych liczbami rzymskimi od I do VIII na poniższym rysunku):

Warszawa, 19-20 października 2013 r.